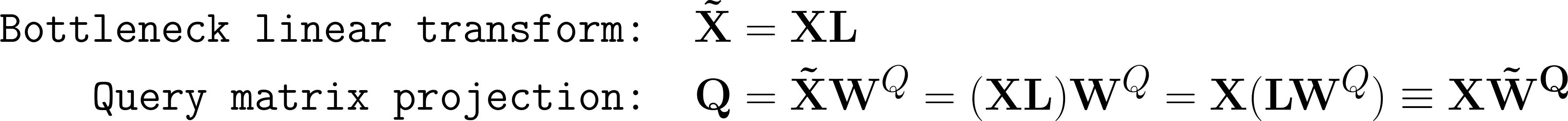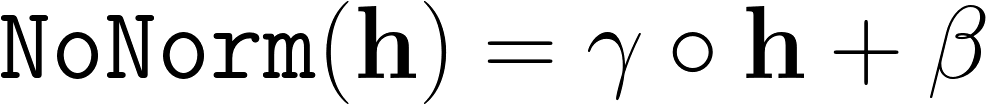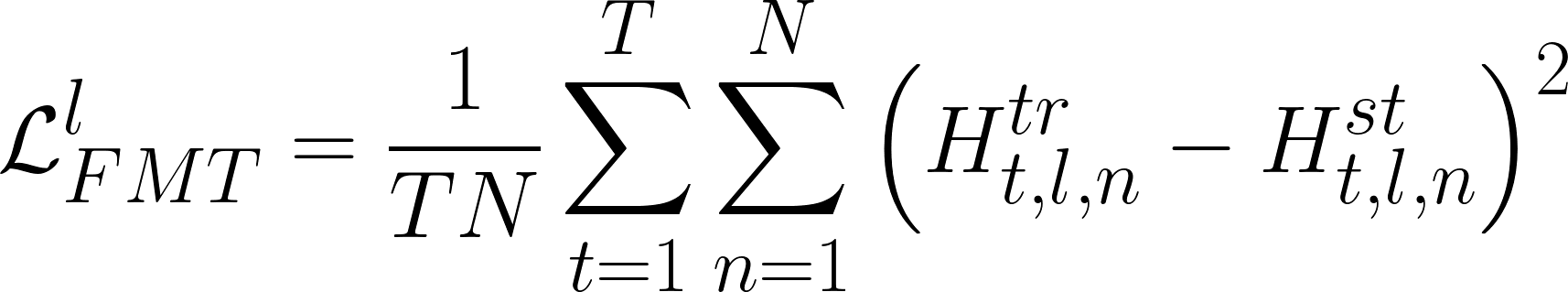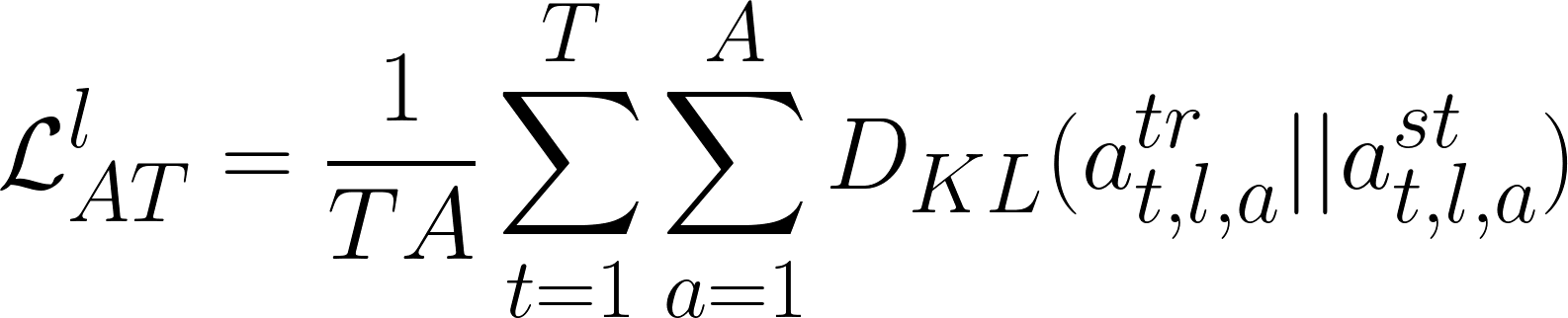Overview
As the size of the NLP model increases into the hundreds of billions of parameters, so does the importance of being able to create more compact representations of these models. Knowledge distillation has successfully enabled this but is still considered an afterthought when designing the teacher models. This probably reduces the effectiveness of the distillation, leaving potential performance improvements for the student on the table.
Further, the difficulties in fine-tuning small student models after the initial distillation, without degrading their performance, requires us to both pre-train and fine-tune the teachers on the tasks we want the student to be able to perform. Training a student model through knowledge distillation will, therefore, require more training compared to only training the teacher, which limits the benefits of a student model to inference-time.
What would be possible if, instead, knowledge distillation was put front and center during the design and training of the teacher model? Could we design and successfully train a model that is supposed to be distilled and could the distilled version successfully be fine-tuned? These are some of the questions addressed in MobileBERT: a Compact Task-Agnostic BERT for Resource-Limited Devices which this article will provide a summary of.
Introduction
Knowledge distillation allows the representational power learned by one model (the teacher) to be distilled into a smaller one (the student). This has shown promising results in previous work, wherein one instance 96% of the teacher’s performance was retained in a 7x smaller model. While an impressive feat, there is still room for improvement where two of the main points are outlined below.
1). Dimensionality reduction is required to compare teacher representations with the students
This comparison lies at the core of most knowledge distillation procedures — we need some way of nudging the student’s activations closer to its teacher. One such way is to minimize the difference between teacher- and student representation at one or more places in the architecture. DistillBERT achieves this by in part minimizing the cosine distance between the inter-transformer block embedding of the two models.
A distance measure such as this one requires both terms to be of the same dimension. In the case of DistillBERT, teacher and student only differ in the number of layers, all other architectural parameters remain the same. If that would not have been the case, then a different approach would have been needed, which is the case for TinyBERT. There the dimensionality reduction was achieved through a mapping matrix learned during distillation. While this approach is flexible, as it allows student model to be of whatever size we choose, it still considers distillation as an afterthought. Understandably, this approach is tempting when there already are state of the art models available but might nonetheless be sub-optimal.
2). Difficult to fine-tune student model on down-stream task after distillation from the teacher
To achieve competitive performance on specific tasks with a model like TinyBERT require us to both pre-train and fine-tune its teacher on this particular task. The reason for this lies in the fact that it is difficult to fine-tuning a student of this size due to its limited capacity. Actually creating a distilled model will, therefore, require more compute compared to its teacher counterpart. This might not pose an issue if the end goal of the training process is to produce a fast and light model to be used on computing limited devices such as a smartphone.
But if our goal is to enable us to fine-tune a distilled student model on any task, then we would have fallen short. To achieve this, we would need to create a general or task-agnostic distilled model that could be dealt with as any other pre-trained transformer model. Just like a pre-trained BERT model is a great starting point for a variety of NLP tasks, this imaginary student model would provide the exact same benefits. Just in a smaller form factor. This in and of itself is the main benefit — a smaller model allows for faster training iteration, even on cheap hardware, which enables more researchers, companies, and enthusiasts to utilize this technology!
The problems outlined above are in part what the team at Google Brain address in their paper MobileBERT. In the following sections, we will go through their contributions in detail to understand how these address the problems above.
The MobileBERT architectures
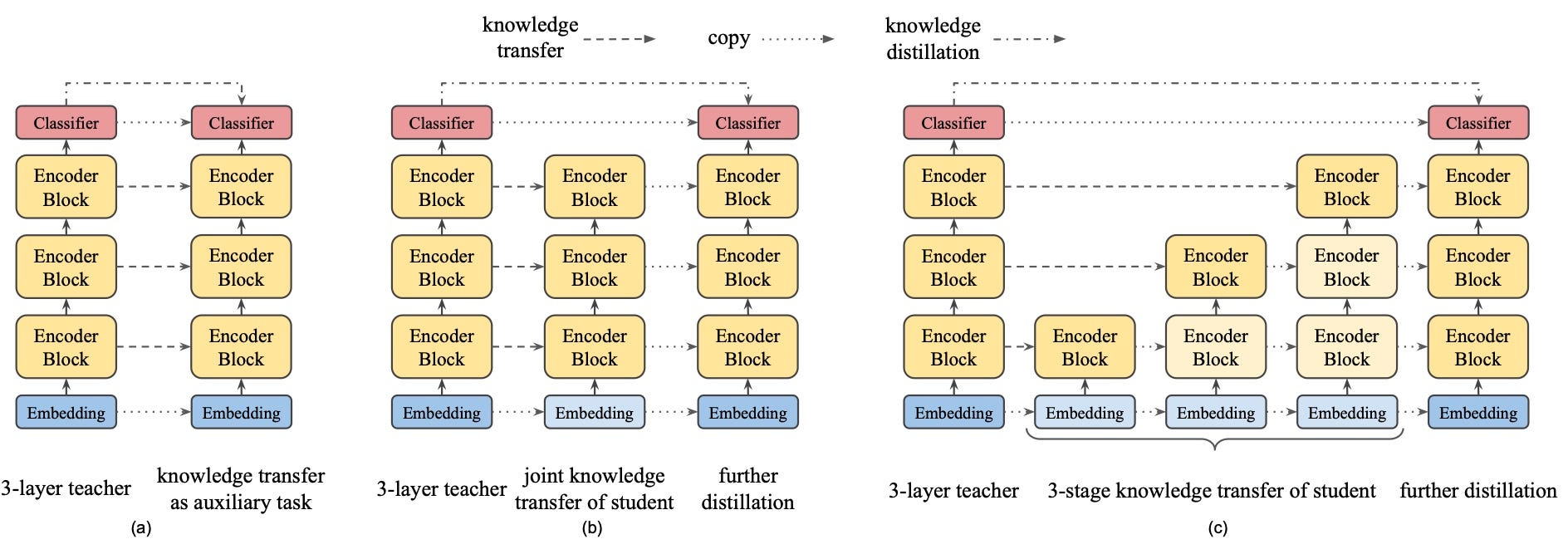
To solve the first issue outlined above, the authors propose a modification to the vanilla BERT transformer blocks they refer to as bottlenecks and inverted bottlenecks. Let’s see how these are incorporated.
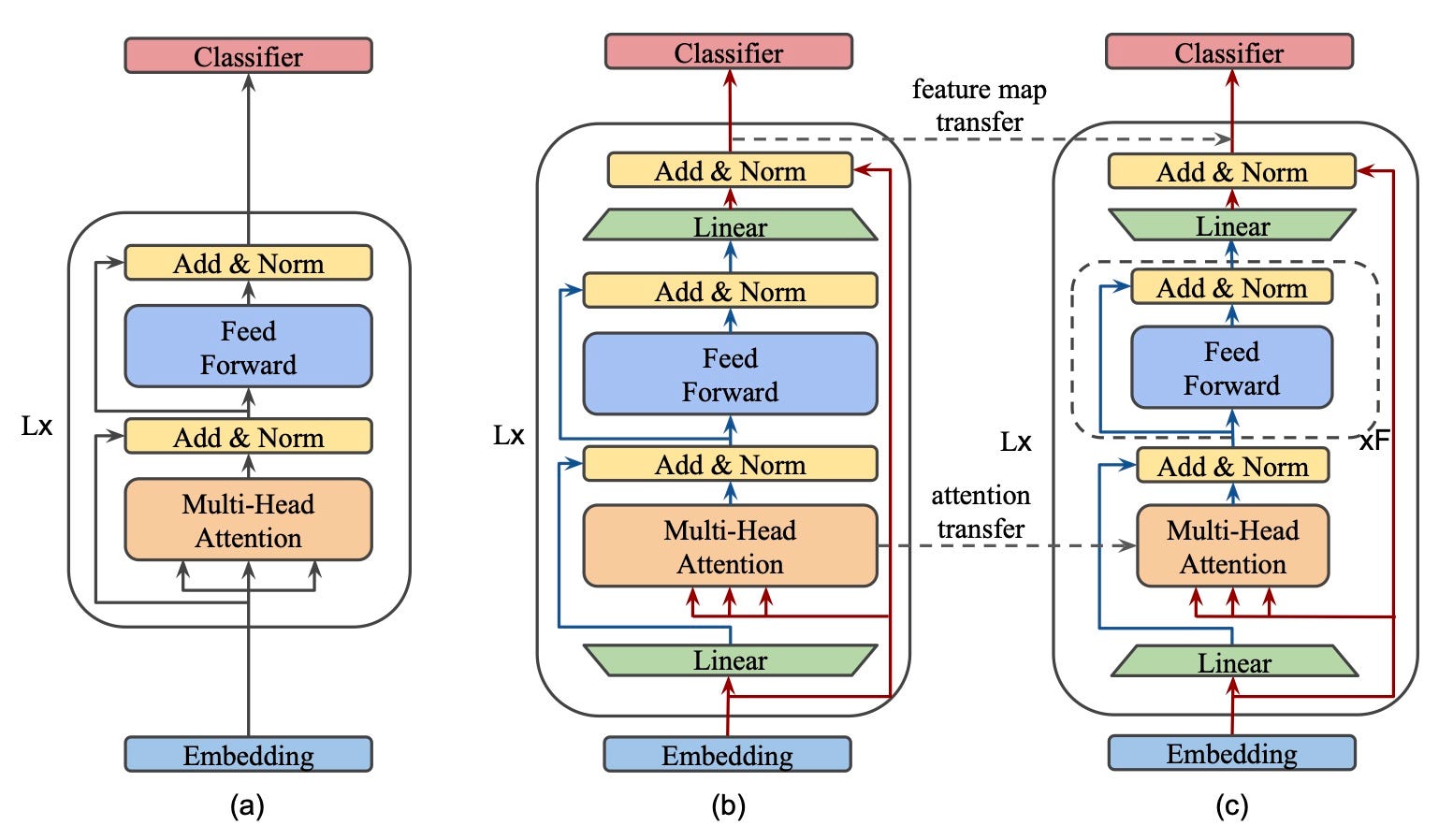
(a) represents your ordinary BERT consisting of L transformer encoder blocks, each, in turn, using a Multi-Head Attention (MHA), skip-connections with normalization (Add & Norm) and Feed-Forward Networks (FFN) to enrich the input representations. If these elements are not familiar with you, this is the go-to illustration of those concepts.
(b) and (c) represents the teacher and student architectures respectively in the proposed distillation scheme. There is obviously much more going on inside each transformer block here but should make sense if we study one element at a time.
Linear
The first, and second to last, element in both student and teacher architectures is a linear transform (the bottlenecks referred to earlier). These serve one single purpose — change the input dimension. The input is projected to match the dimensions of the internal representations of their respective model, while the output is projected to match the inter-block representation size. In the teacher case, this projects input from 512 to 1024 while the student reduces the input dimension from 512 to 128. What is important to note here is that both teacher’s inverted bottleneck and student’s bottleneck are fed the same input dimension 512. This is key for multiple reasons in this proposed knowledge distillation framework.
- With the same input dimension to all transformer blocks, it’s trivial to incorporate distillation losses aimed at minimizing the difference between a teacher and student representations. I’ll leave the details of this loss function for later, just remember that the bottlenecks are what enables these.
- The same input, and output, dimension also means that “Embedding” and “Classifier” layers will be compatible with both models. There is, therefore, no reason to try to learn these layers through some kind of optimization process since they can be copied from teacher to student!
Multi-Head Attention
Moving forward in the architecture, we come to the MHA block. The observant reader will have noticed that the input to this block is not the output from the prior linear projection. Instead, the initial input is used. There is no motivation for this design choice in the paper, which leaves us to speculate. I believe the reason is the increased dimensions of freedom it allows. Let me explain.
By not using the result of the linear projection as input to the MHA block, we allow the model to de-couple how it deals with the information that passes through the MHA block and that which re-connects with this block’s output. Another argument for this approach is the fact that, mathematically, the input to the MHA-block would remain the same regardless of which alternative is chosen. This is true because the first thing that happens in this block is a linear projection to create the key, query, and value vectors of each head, which means that any prior linear transforms could be “baked” into these ones. Please follow the below example equations.
This shows us that it using the output from the linear projection does not change the behavior of the MHA block, and at best limit its capabilities.
For a second, let’s focus solely on the teacher. If we continuing the path past the MHA-block, things remain the same compared to a vanilla transformer block until we reach the second “Add & Norm” operation. After this layer, we have a bottleneck transform, this time to reduce the dimension back to that of the input. This allows us to perform another Add & Norm operation with the transformer block input before feeding the result onto the next block.
Stacked FFN
Let’s move our attention to (c), the student, in the figure above. The same analysis as above holds true up until the Add & Norm operation after MHA, after which the authors introduce what they call stacked FFN. This repeats the Feed Forward + Add & Norm blocks 4 times, all of which might seems very peculiar. Their reasoning here has to do with the parameter ratio between MHA and FFN-blocks. In BERT this ratio was exactly 0.5, meaning that the FFN block had twice the number of parameters compared to the MHA block.
However, in BERT both these blocks were fed the same dimensional input, which is not the case for the bottleneck architecture of MobileBERT. Further, this ratio was most certainly selected for good reason, as ablation studies in this work verify that the best performance is achieved when the ratio is in the range of 0.4–0.6. The solution for achieving this parameter ratio with much smaller FFN blocks was therefore to stack a sufficient number of these FFN blocks.
Operational optimizations
Due to one of the goals being to enable fast inference on resource-limited devices did the authors identify two areas where their architecture could be further improved. First of all the authors replaced the smooth GeLU activation function for ReLU, and secondly did they re-think the normalization operation. The proposed alternative is a simple element-wise linear transformation expressed as:
Ablations show that both these changes improve inference time by a significant margin — more than 3 times! These simplifications do however come at the cost of reduced performance, as will be shown later.
The motivation of teacher and student size
Almost all parameters selected for these models might seem a bit arbitrary unless I explain the initial design goals. For the teacher, the starting point was BERT-large: 24 transformer blocks, each with 16 attention heads and an internal representation of 1024. The goal was then to keep the inter-block hidden representations (the input dimension to the initial bottleneck) as small as possible without sacrificing performance. Ablation studies showed that this could be reduced to 512 without a significant drop in performance.
The starting point for the student was to create a 25M parameters model. However, the distillation process (which I will explain in the next section) requires that the number of transformer layers and inter-block hidden representation dimensions are kept the same as the teacher. MobileBERT is therefore required to have 24 layers and an input dimension of 512. This leaves three parameters to play with; the internal representation dimension, the number of attention heads, and the number of stacked FFNs. All these had to be balanced to stay within the parameter budget while both achieving a good parameter ratio between MHA and FFN and training performance.
The best performing configuration was achieved for an internal representation of 128, 4 attention heads and 4 stacked FFN’s. Due to the distillation process explained below, this requires the teacher to also use 4 attention heads. Fortunately, ablations show that reducing from 16 heads to 4 does not impact performance significantly.
Proposed knowledge distillation objectives
All the architectural modifications are created with the intention of allowing knowledge distillation between student and teacher. For this, the authors propose two training objectives:
Feature map transfer —
Allows the student to mimic the teacher at each transformer layer output. It the architecture image, this is shown as a dashed arrow between the output of the models. The objective function to minimize is defined as the mean square error between the feature maps.
Attention map transfer —
Which tokens the teacher attends to at different layers and heads is another important property we want the student to learn. This is enabled by minimizing the difference between the attention distributions (the KL-divergence) at each layer and head.
With these objectives, there is more than one way we can perform knowledge distillation. The authors propose three alternatives:
- Auxiliary knowledge transfer — The layer-wise knowledge transfer objectives are minimized together with the main objectives — masked language modeling and next sentence prediction. This can be considered the most simple approach.
- Joint knowledge transfer — Instead of trying to achieve all objectives at once, it is possible to separate knowledge distillation and pre-training into two stages of training. First, all layer-wise knowledge distillation losses are trained until convergence and then further training with the pre-training objective is performed.
- Progressive knowledge transfer — The two-step approach can be taken even further. Errors not yet minimized properly in early layers will propagate and affect the training of later layers if all layers are trained simultaneously. It might, therefore, be better to train one layer at a time while freezing or reducing the learning rate of previous layers
Experimental results
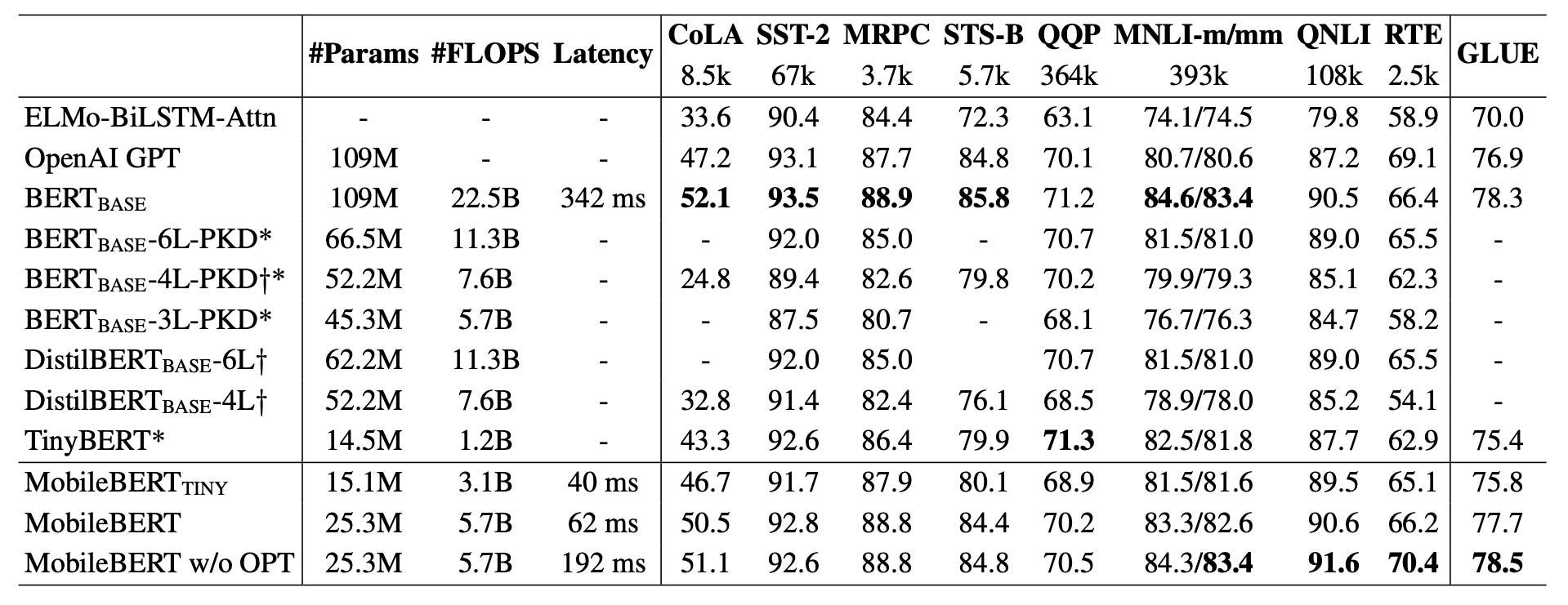
We’ve come a long way to finally figure out if all this actually works in practice. The authors evaluate their proposed MobileBERT in three configurations; the main model with 25M parameters (MobileBERT), the same model without the operational optimizations (MobileBERT w/o OPT), as well as a model with only 15M parameters (MobileBERT-tiny).
These models were compared to both baseline algorithms such as ELMo, GPT, and BERT-base as wells as related distillation work: BERT-PKD, DistilBERT, and TinyBERT.
What we find is that MobileBERT w/ o OPT outperforms the much larger BERT-base by 0.2 average GLUE score, while being 4x smaller. MobileBERT on the other hand, which includes the proposed operational optimizations, drops 0.8 GLUE score for a much faster inference time, 62 ms for a sequence of 128 tokens on a Pixel 4 phone! Its performance is however still competitive since it outperforms GTP and ELMo by a significant margin.
It’s, therefore, safe to conclude that it’s possible to create a distilled model which both can be performant and fast on resource-limited devices!
MobileBERT-tiny achieves slightly better performance compared to TinyBERT. This does however become even more impressive when you consider how TinyBERT was fine-tuned for the GLUE tasks. Remember, prior to this work it was not possible to fine-tune the students due to their small capacity. TinyBERT’s teacher BERT-base, therefore, had to be fine-tuned before its knowledge could be distilled into TinyBERT! That is not the case for MobileBERT.
It’s been fine-tuned by itself on GLUE which proves that it’s possible to create a task agnostic model through the proposed distillation process!
Another fact that becomes apparent from this comparison is that the model capacity might no longer be the limiting factor. Rather, its the pre-training procedure that is. There have already been developments in regards to more effective pre-training processes where ELECTRA provides an illustrating example.
Conclusion
If you’ve made it this far, you deserve a high-five. Current state-of-the-art NLP models almost grow by the minute, which makes it difficult to apply them in production. Knowledge distillation provides tools for addressing this particular issue but brings its own set of new challenges. Two of these are discussed in this article; “knowledge distillation is an afterthought when designing teacher models” and “knowledge distillation cannot produce general, task agnostic models”.
MobileBERT introduces bottlenecks in the transformer blocks, which allows us to more easily distill the knowledge from larger teachers into smaller students. This technique reduces the width rather than the depth of the student, which is known to produce a more capable model, which holds true in the provided experiments. MobileBERT highlights the fact that it’s possible to create a student model that by itself can be fine-tuned after the initial distillation process!
Further, the results also show that this holds true in practice too as MobileBERT is able to reach 99.2% of BERT-base’s performance on GLUE with 4x fewer parameters and 5.5x faster inference on a Pixel 4 phone!
If you found this summary helpful in understanding the broader picture of this particular research paper, please consider reading my other articles! I’ve already written a bunch and more will definitely be added. I think you might find this one interesting👋🏼🤖
About the Author

I am a Software Engineer and MSc of Machine Learning with a growing interest in NLP. Trying to stay on top of recent developments within the ML field in general, and NLP in particular. Writing to learn!