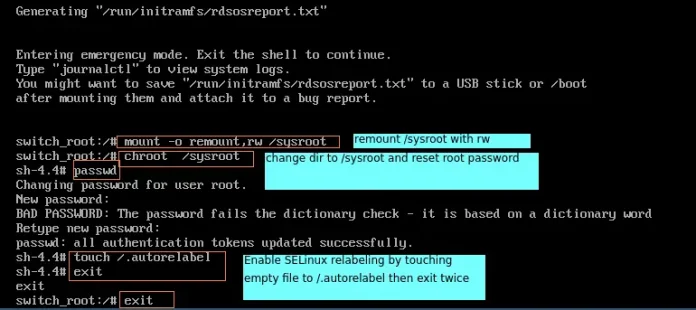
Given here is an equilateral triangle of side length a, which inscribes a hexagon which in turn inscribes a square. The task is to find the side length of the square.
Examples:
Input: a = 6 Output: 2.538 Input: a = 8 Output: 3.384
Approach:
We know the, side length of a hexagon inscribed within an equilateral triangle is h = a/3. Please refer Largest hexagon that can be inscribed within an equilateral triangle .
Also, the side length of the square that can be inscribed within a hexagon is x = 1.268h Please refer Largest Square that can be inscribed within a hexagon.
So, side length of the square inscribed within a hexagon which in turn is inscribed within an equilateral triangle, x = 0.423a.
Below is the implementation of the above approach:
C++
// C++ program to find the side of the largest square// that can be inscribed within the hexagon which in return// is incsribed within an equilateral triangle#include <bits/stdc++.h>using namespace std;// Function to find the side// of the squarefloat squareSide(float a){ // Side cannot be negative if (a < 0) return -1; // side of the square float x = 0.423 * a; return x;}// Driver codeint main(){ float a = 8; cout << squareSide(a) << endl; return 0;} |
Java
// Java program to find the side of the// largest square that can be inscribed // within the hexagon which in return is // incsribed within an equilateral triangleclass cfg { // Function to find the side// of the squarestatic float squareSide(float a){ // Side cannot be negative if (a < 0) return -1; // side of the square float x = (0.423f * a); return x;}// Driver codepublic static void main(String[] args){ float a = 8; System.out.println(squareSide(a));}}// This code is contributed by // Mukul Singh. |
Python3
# Python 3 program to find the side of the # largest square that can be inscribed # within the hexagon which in return# is incsribed within an equilateral triangle# Function to find the side of the squaredef squareSide(a): # Side cannot be negative if (a < 0): return -1 # side of the square x = 0.423 * a return x# Driver codeif __name__ == '__main__': a = 8 print(squareSide(a))# This code is contributed by# Sanjit_Prasad |
C#
// C# program to find the side of the// largest square that can be inscribed // within the hexagon which in return is // incsribed within an equilateral triangleusing System;class GFG{ // Function to find the side// of the squarestatic float squareSide(float a){ // Side cannot be negative if (a < 0) return -1; // side of the square float x = (0.423f * a); return x;}// Driver codepublic static void Main(){ float a = 8; Console.WriteLine(squareSide(a));}}// This code is contributed by // shs |
PHP
<?php// PHP program to find the side of the // largest square that can be inscribed // within the hexagon which in return is// incsribed within an equilateral triangle// Function to find the side of the squarefunction squareSide($a){ // Side cannot be negative if ($a < 0) return -1; // side of the square $x = 0.423 * $a; return $x;}// Driver code$a = 8;echo squareSide($a);// This code is contributed by ajit.?> |
Javascript
<script>// javascript program to find the side of the// largest square that can be inscribed // within the hexagon which in return is // incsribed within an equilateral triangle// Function to find the side// of the squarefunction squareSide(a){ // Side cannot be negative if (a < 0) return -1; // side of the square var x = (0.423 * a); return x;}// Driver codevar a = 8;document.write(squareSide(a));// This code is contributed by Princi Singh </script> |
3.384
Time Complexity: O(1) since no loop is used the algorithm takes constant time to finish its execution
Auxiliary Space: O(1) since no extra array is used the space required by the algorithm to complete is constant.
Ready to dive in? Explore our Free Demo Content and join our DSA course, trusted by over 100,000 neveropen!