Implementation of Exact Cover Problem and Algorithm X using DLX

In the article Exact Cover Problem and Algorithm X | Set 1 we discussed the Exact Cover problem and Algorithm X to solve the Exact cover problem. In this article, we’ll discuss the implementation details of Algorithm X using Dancing Links Technique (DLX) proposed by Dr Donald E. Knuth in his paper “Dancing Links”

Dancing Link Technique

Dancing link technique relies on the idea of doubly circular linked list. As discussed in previous article, we transform exact cover problem in form of matrix of 0 and 1. Here each “1” in the matrix is represented by a node of linked list and the whole matrix is transformed into a mesh of 4 way connected nodes. Each node contains following fields –

• Pointer to node left to it
• Pointer to node right to it
• Pointer to node above it
• Pointer to node below it
• Pointer to list header node to which it belongs

Each row of the matrix is thus a circular linked list linked to each other with left and right pointers and each column of the matrix will also be circular linked list linked to each above with up and down pointer. Each column list also includes a special node called “list header node”. This header node is just like simple node but have few extra fields –

• Column id
• Count of nodes in current column

We can have two different kinds of nodes but in our implementation, we will create only one kind of node with all fields for convenience with an additional “Row id” field which will tell which row this node belongs to. So for matrix – The 4-way linked matrix will look like this –

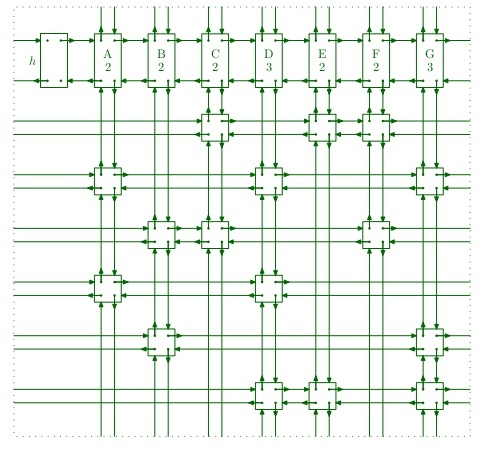
Four way linked matrix

So the pseudo code for search algorithm (Algorithm X) will be –

f( h.right == h ) { 
     printSolutions(); 
     return; 
} 
else { 
     ColumnNode column = getMinColumn(); 
     cover(column); 

     for( Node row = column.down ; rowNode != column ;
        rowNode = rowNode.down ) { 
            solutions.add( rowNode ); 

            for( Node rightNode = row.right ; rightNode != row ;
                 rightNode = rightNode.right ) 
                    cover( rightNode ); 

     Search( k+1); 
     solutions.remove( rowNode ); 
     column = rowNode.column; 

     for( Node leftNode = rowNode.left ; leftNode != row ;
              leftNode = leftNode.left )                                                                             
            uncover( leftNode ); 
     } 
     uncover( column ); 
} 

Covering Node

As discussed in the algorithm, we have to remove columns and all the rows to which nodes of that column belongs to. This process is here referred as covering of node. To remove a column we can simply unlink header of that column from neighboring headers. This way this column cannot be accessed. This process is similar to removal of node from doubly linked list, suppose we want to remove node x then –

x.left.right = x.right
x.right.left = x.left

Similarly to remove a row we have to unlink all nodes of row from nodes of row above and below it.

x.up.down = x.down
x.down.up = x.up

Thus the pseudo code for cover(node) becomes –

Node column = dataNode.column; 

column.right.left = column.left; 
column.left.right = column.right; 

for( Node row = column.down ; row != column ; row = row.down ) 
    for( Node rightNode = row.right ; rightNode != row ; 
         rightNode = rightNode.right ) { 
         rightNode.up.down = rightNode.down; 
         rightNode.down.up = rightNode.up; 
    } 
} 

So for example, after covering column A, matrix will look like this –

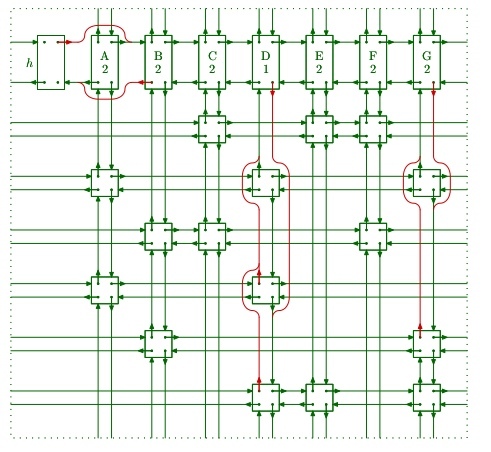
covering

Here we first remove the column from other columns then we move down to each column node and remove row by traversing right, so row 2 and 4 is removed.

Uncovering Node

Suppose algorithm reached a dead end and no solution is possible in that case algorithm have to backtrack. Because we have removed columns and rows when we backtrack we have link again those removed rows and columns. This is what we are calling uncovering. Notice that the removed nodes still have pointers to their neighbors, so we can link them back again using these pointers. To uncover column we will perform covering operation but in reverse order –

x.left.right = x
x.right.left = x

Similarly to uncover any row node x –

x.up.down = x
x.down.up = x

Thus the pseudo code for uncover(node) will become –

Node column = dataNode.column; 

for( Node row = column.up ; row != column ; row = row.up ) 
    for( Node leftNode = row.left ; leftNode != row ;
         leftNode = leftNode.right ) { 
         leftNode.up.down = leftNode; 
         leftNode.down.up = leftNode; 
     } 
column.right.left = column; 
column.left.right = column; 
} 

Following is the implementation of dancing link technique – 

Output:

Printing Solutions: 6 4 2 
Printing Solutions: 6 4 7

The time complexity of the createToridolMatrix() function is O(n^2), where n is the number of rows and columns in the ProbMat array. This is because the function iterates through every element in the ProbMat array and creates a new node for each element that is equal to 1.

The space complexity of the createToridolMatrix() function is also O(n^2), since it creates a new node for each element in the ProbMat array that is equal to 1.

The time and space complexity of the remaining functions in the program depend on the specific implementation of the DLX algorithm and the specific problem being solved. However, in general, the time complexity of the DLX algorithm is exponential in the worst case, although it often performs much better in practice. The space complexity of the DLX algorithm is generally linear in the size of the input.

References

• https://www.ocf.berkeley.edu/%7Ejchu/publicportal/sudoku/sudoku.paper.html
• Dancing Links by Donald Knuth

This article is contributed by Atul Kumar. If you like neveropen and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the neveropen main page and help other Geeks. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.