Underfitting and Overfitting in Machine Learning

Introduction

Underfitting and overfitting are two common challenges faced in machine learning. Underfitting happens when a model is not good enough to understand all the details in the data. It’s like the model is too simple and misses important stuff.. This leads to poor performance on both the training and test sets. Overfitting, on the other hand, occurs when a model is too complex and memorizes the training data too well. This leads to good performance on the training set but poor performance on the test set.

In this blog post, we will discuss the reasons for underfitting and overfitting.

What is Underfitting?

Overfitting happens when a machine learning model becomes overly intricate, essentially memorizing the training data. While this might lead to high accuracy on the training set, the model may struggle with new, unseen data due to its excessive focus on specific details.

Reasons for Underfitting

• Too few features miss important details.
• Using a simple model for a complex problem.
• Excessive regularization limits model flexibility.

What is Overfitting?

Underfitting occurs when a model is too simplistic to grasp the underlying patterns in the data. It lacks the complexity needed to adequately represent the relationships present, resulting in poor performance on both the training and new data.

Reasons for Overfitting

• Too many features confuse the model.
• Using a complex model for a simple problem.
• Not enough regularization.

The Challenge of Underfitting and Overfitting in Machine Learning

You’ll inevitably face this question in a data scientist interview:

Can you explain what is underfitting and overfitting in the context of machine learning? Describe it in a way even a non-technical person will grasp.

Your ability to explain this in a non-technical and easy-to-understand manner might well decide your fit for the data science role!

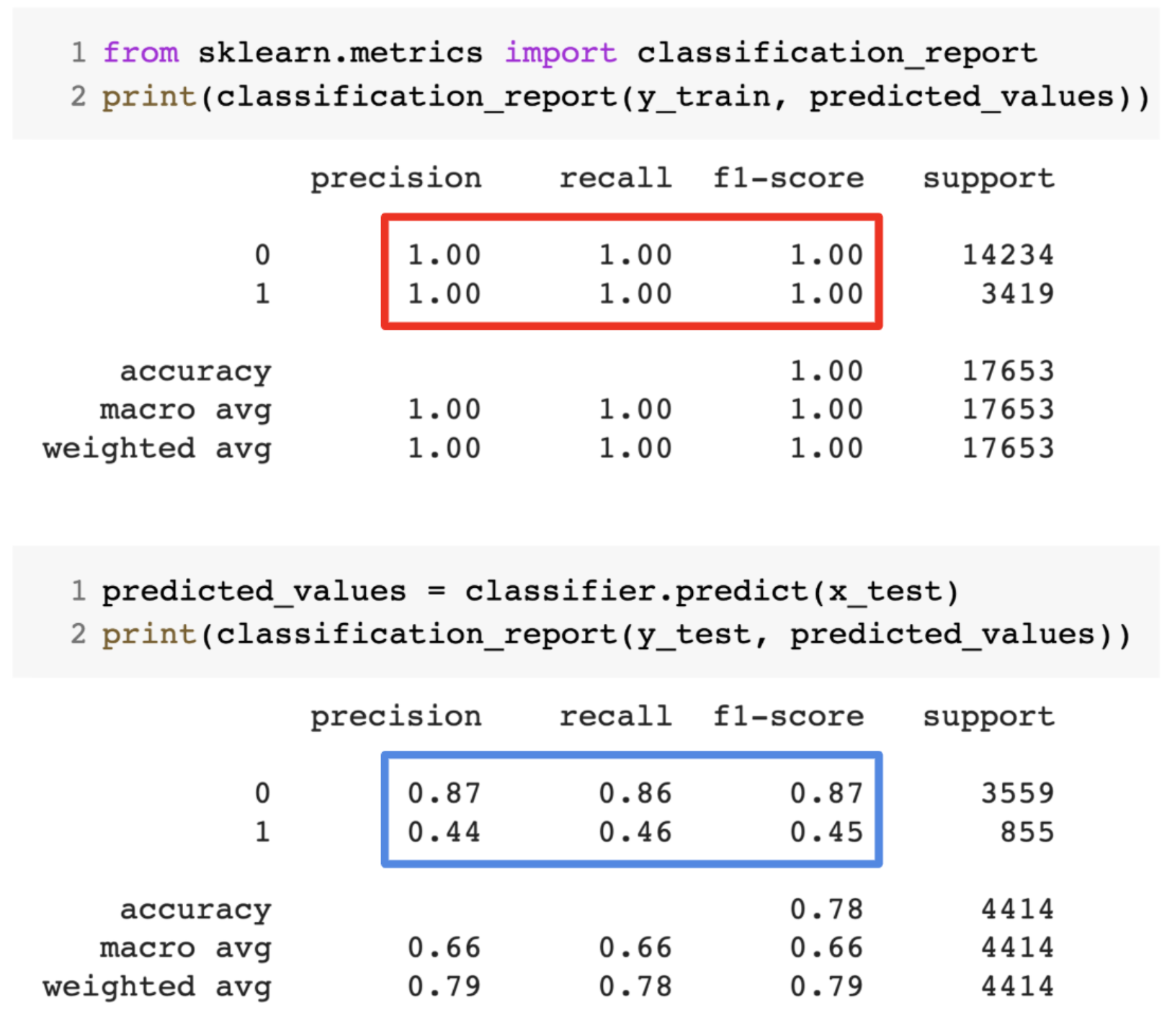
Even when we’re working on a machine learning project, we often face situations where we are encountering unexpected performance or error rate differences between the training set and the test set (as shown below). How can a model perform so well over the training set and just as poorly on the test set?

This happens very frequently whenever I am working with tree-based predictive models. Because of the way the algorithms work, you can imagine how tricky it is to avoid falling into the overfitting trap!

Moreover, it can be quite daunting when we are unable to find the underlying reason why our predictive model is exhibiting this anomalous behavior.

Here’s my personal experience – ask any seasoned data scientist about this, they typically start talking about some array of fancy terms like Overfitting, Underfitting, Bias, and Variance. But little does anyone talk about the intuition behind these machine learning concepts. Let’s rectify that, shall we?

Let’s Take an Example to Understand Underfitting vs. Overfitting

I want to explain these concepts using a real-world example. A lot of folks talk about the theoretical angle but I feel that’s not enough – we need to visualize how underfitting and overfitting actually work.

So, let’s go back to our college days for this.

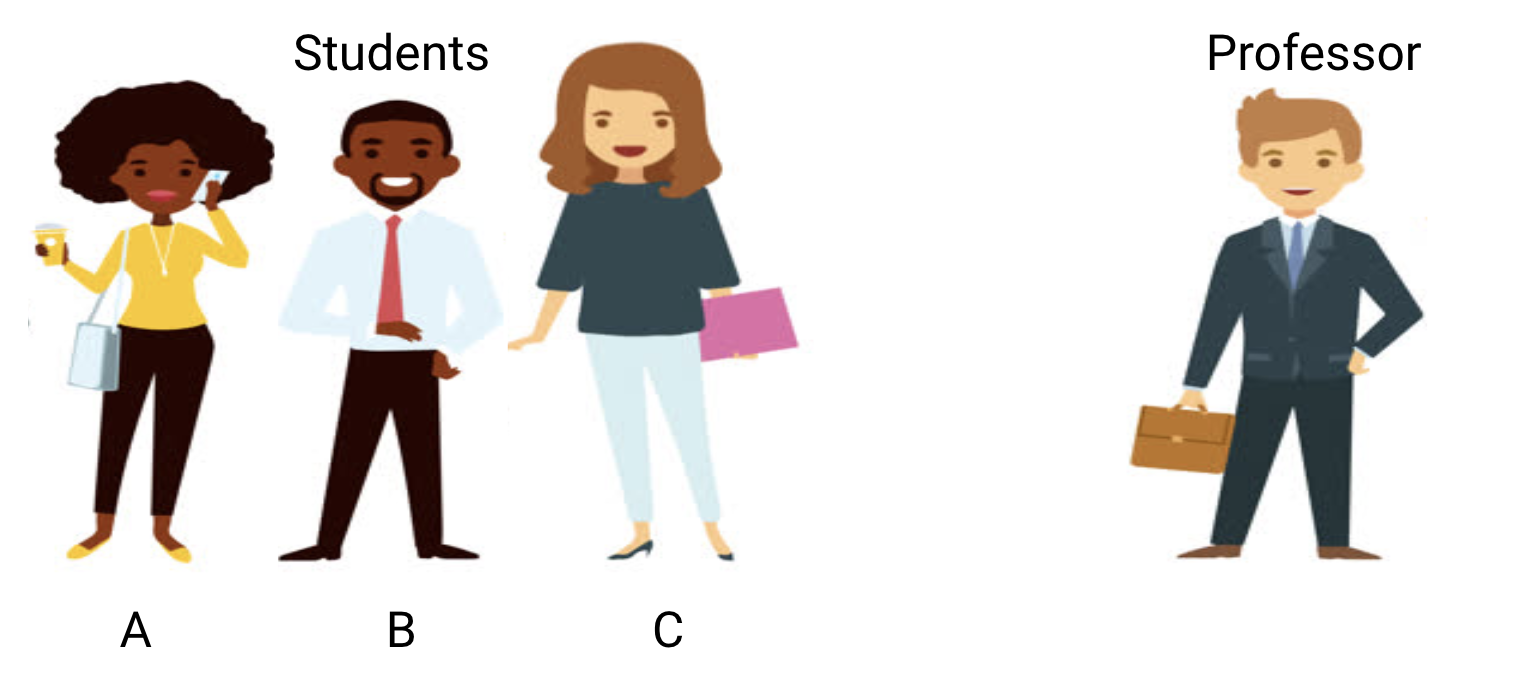
Consider a math class consisting of 3 students and a professor.

Now, in any classroom, we can broadly divide the students into 3 categories. We’ll talk about them one-by-one.

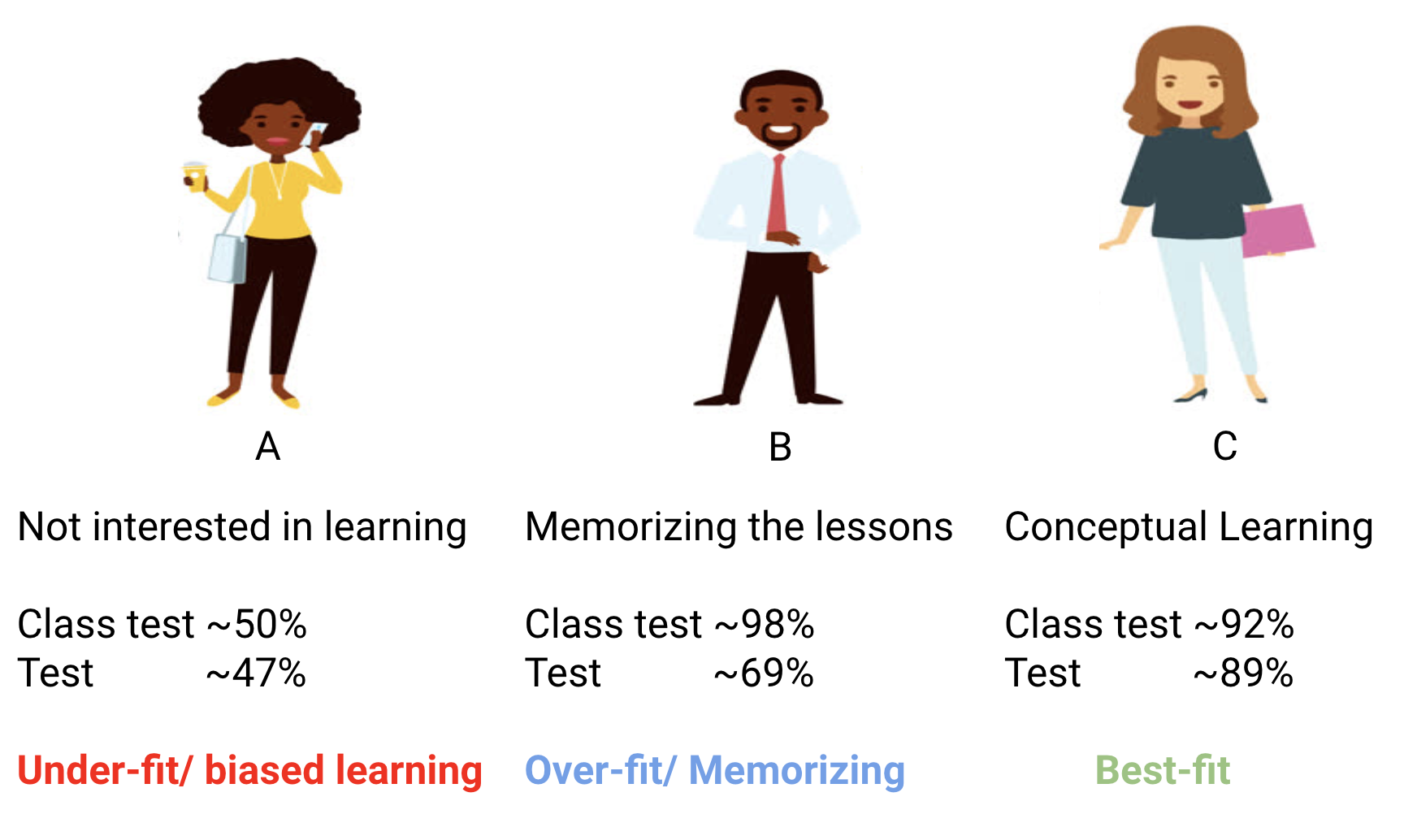
Let’s say that student A resembles a student who does not like math. She is not interested in what is being taught in the class and therefore does not pay much attention to the professor and the content he is teaching.

Let’s consider student B. He is the most competitive student who focuses on memorizing each and every question being taught in class instead of focusing on the key concepts. Basically, he isn’t interested in learning the problem-solving approach.

Finally, we have the ideal student C. She is purely interested in learning the key concepts and the problem-solving approach in the math class rather than just memorizing the solutions presented.

We all know from experience what happens in a classroom. The professor first delivers lectures and teaches the students about the problems and how to solve them. At the end of the day, the professor simply takes a quiz based on what he taught in the class.

The obstacle comes in the semester3 tests that the school lays down. This is where new questions (unseen data) comes up. The students haven’t seen these questions before and certainly haven’t solved them in the classroom. Sounds familiar?

So, let’s discuss what happens when the teacher takes a classroom test at the end of the day:

• Student A, who was distracted in his own world, simply guessed the answers and got approximately 50% marks in the test
• On the other hand, the student who memorized each and every question taught in the classroom was able to answer almost every question by memory and therefore obtained 98% marks in the class test
• For student C, she actually solved all the questions using the problem-solving approach she learned in the classroom and scored 92%

We can clearly infer that the student who simply memorizes everything is scoring better without much difficulty.

Now here’s the twist. Let’s also look at what happens during the monthly test, when students have to face new unknown questions which are not taught in the class by the teacher.

• In the case of student A, things did not change much and he still randomly answers questions correctly ~50% of the time.
• In the case of Student B, his score dropped significantly. Can you guess why? This is because he always memorized the problems that were taught in the class but this monthly test contained questions which he has never seen before. Therefore, his performance went down significantly
• In the case of Student C, the score remained more or less the same. This is because she focused on learning the problem-solving approach and therefore was able to apply the concepts she learned to solve the unknown questions

How Does this Relate to Underfitting and Overfitting in Machine Learning?

You might be wondering how this example relates to the problem which we encountered during the train and test scores of the decision tree classifier? Good question!

So, let’s work on connecting this example with the results of the decision tree classifier that I showed you earlier.

First, the classwork and class test resemble the training data and the prediction over the training data itself respectively. On the other hand, the semester test represents the test set from our data which we keep aside before we train our model (or unseen data in a real-world machine learning project).

Now, recall our decision tree classifier I mentioned earlier. It gave a perfect score over the training set but struggled with the test set. Comparing that to the student examples we just discussed, the classifier establishes an analogy with student B who tried to memorize each and every question in the training set.

Similarly, our decision tree classifier tries to learn each and every point from the training data but suffers radically when it encounters a new data point in the test set. It is not able to generalize it well.

This situation where any given model is performing too well on the training data but the performance drops significantly over the test set is called an overfitting model.

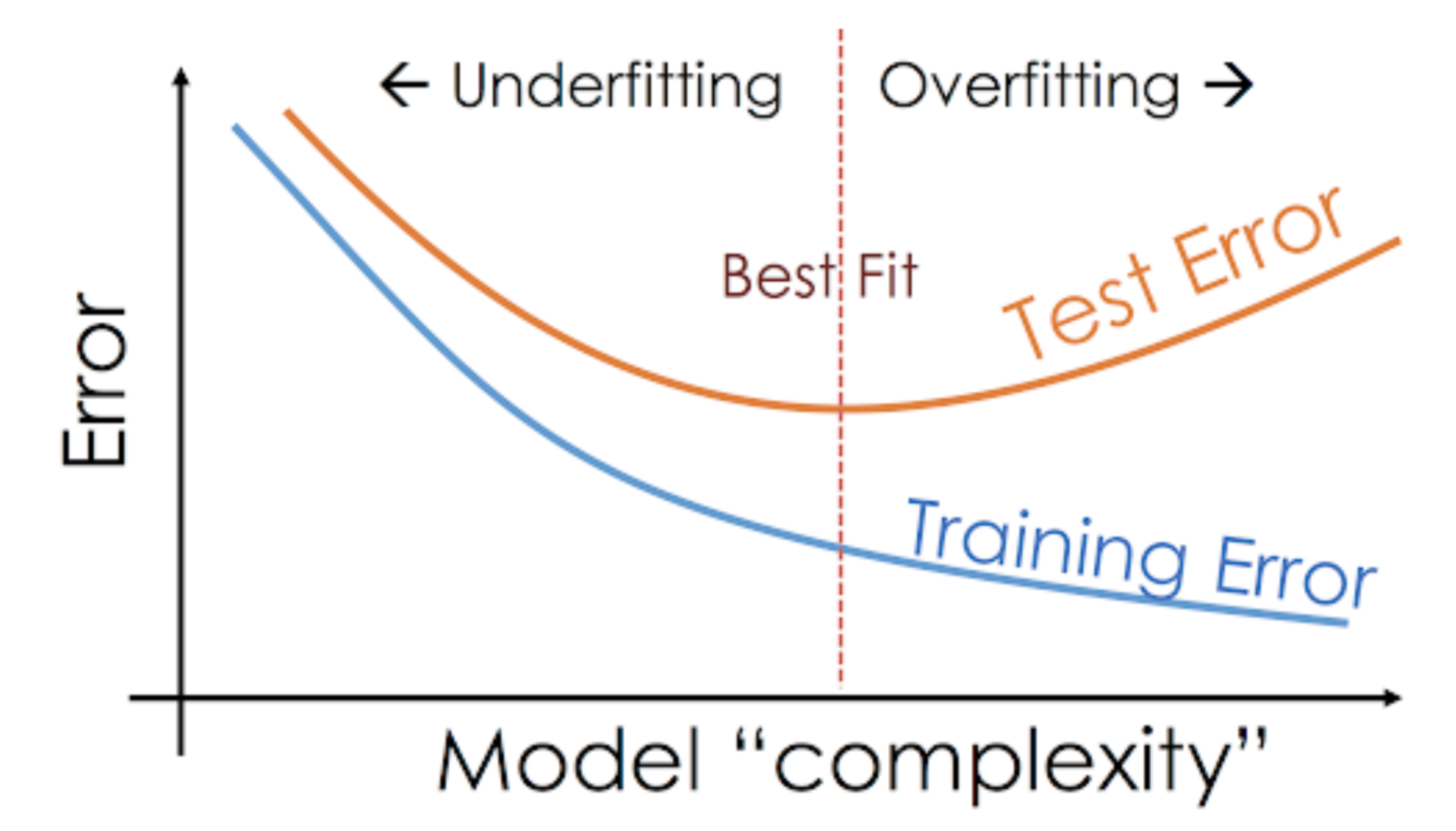
For example, non-parametric models like decision trees, KNN, and other tree-based algorithms are very prone to overfitting. These models can learn very complex relations which can result in overfitting. The graph below summarises this concept:

On the other hand, if the model is performing poorly over the test and the train set, then we call that an underfitting model. An example of this situation would be building a linear regression model over non-linear data.

End Notes

I hope this short intuition has cleared up any doubts you might have had with underfitting, overfitting, and best-fitting models and how they work or behave under the hood.

Feel free to shoot me any questions or thoughts below.

FAQs

Sharoon Saxena

23 Nov 2023