This article was published as a part of the Data Science Blogathon.
Introduction
Model Development is a critical stage in the life cycle of a Data Science project. We attempt to train our data set using various forms of Machine Learning models, either supervised or unsupervised, depending on the Business Problem.
Given many models available for solving business problems, we need to ensure that the model we choose performs effectively on unknown data after this phase. As a result, we cannot rely just on assessment criteria to select the best-performing model.
Apart from the statistic, we want other information to assist us in selecting the final Machine Learning model for deployment to production.
Validation is the process of assessing if the mathematical findings obtained by computing connections between variables are acceptable as representations of the data. Typically, an error estimation for the model is performed after being trained on the train data set, a process known as residual evaluation.
This step calculates the Training Error by comparing the predicted answer to the initial response. However, this statistic cannot be relied upon because it is effective only with training data. It is conceivable that the model is either too small or too large for the data.
Any statistic used to evaluate the model’s performance cannot tell you how well it will perform if applied to an entirely new dataset. It is Cross-Validation, a method that enables us to discover this fact about our model.
This post will learn about the many types of cross-validation procedures, their advantages, and their disadvantages. Let us begin by defining Cross-Validation.
Cross-Validations
Cross-Validations are a resampling strategy that ensures our model’s efficiency and correctness when applied to previously unknown data. It is a technique for assessing Machine Learning models that involves training numerous more Machine Learning models on subsets of the available input data set and evaluating them on the subgroup.
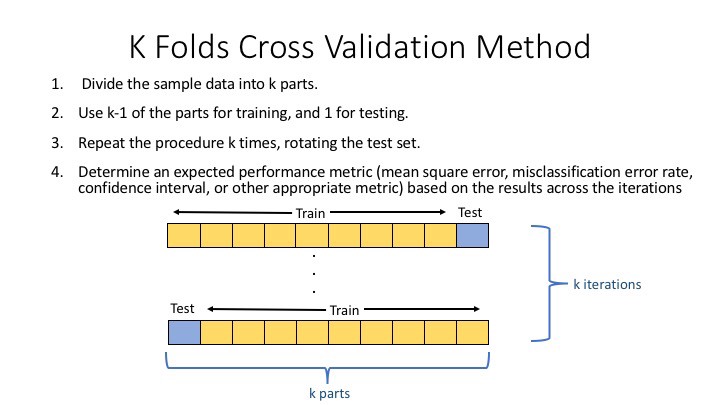
There are several Cross-Validation approaches, but let’s look at the fundamental functionality of Cross-Validation: The first step is to split the cleaned data set into K equal-sized segments.
-
Then, we’ll regard Fold-1 as a test fold and the other K-1 as train folds and compute the test score. fold’s
-
Repeat step 2 for all folds, using another fold as a check while remaining on the train.
-
The final step would be to average the scores of all the folds.
Purpose of Cross-Validations
Types of Cross-Validations
1. Holdout Method
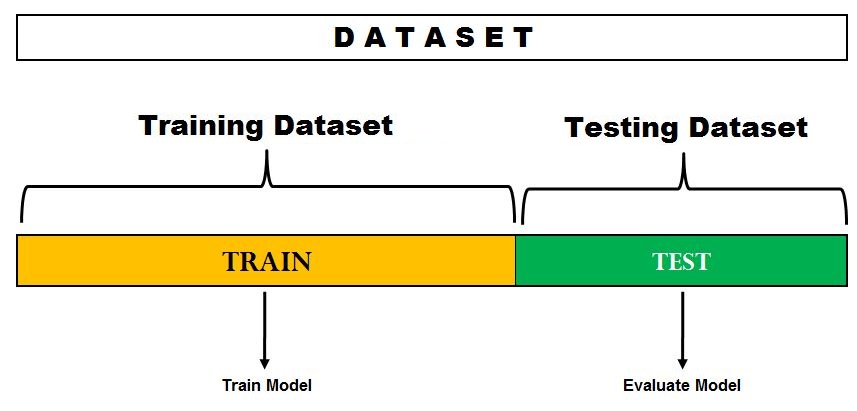
This approach generates predictions by deleting a subset of the training data set and passing it to a trained model on the remaining data set. We next compute the error estimation, which indicates how well our model performs on previously unknown data sets. This is referred to as the Holdout Technique.
Example– Emails in our inbox are classed as spam or not spam.
Pros
- This method is entirely data-independent.
- This method requires only one execution, which results in cheaper computing costs.
Cons
- Due to the lower amount of data, the performance is more variable.
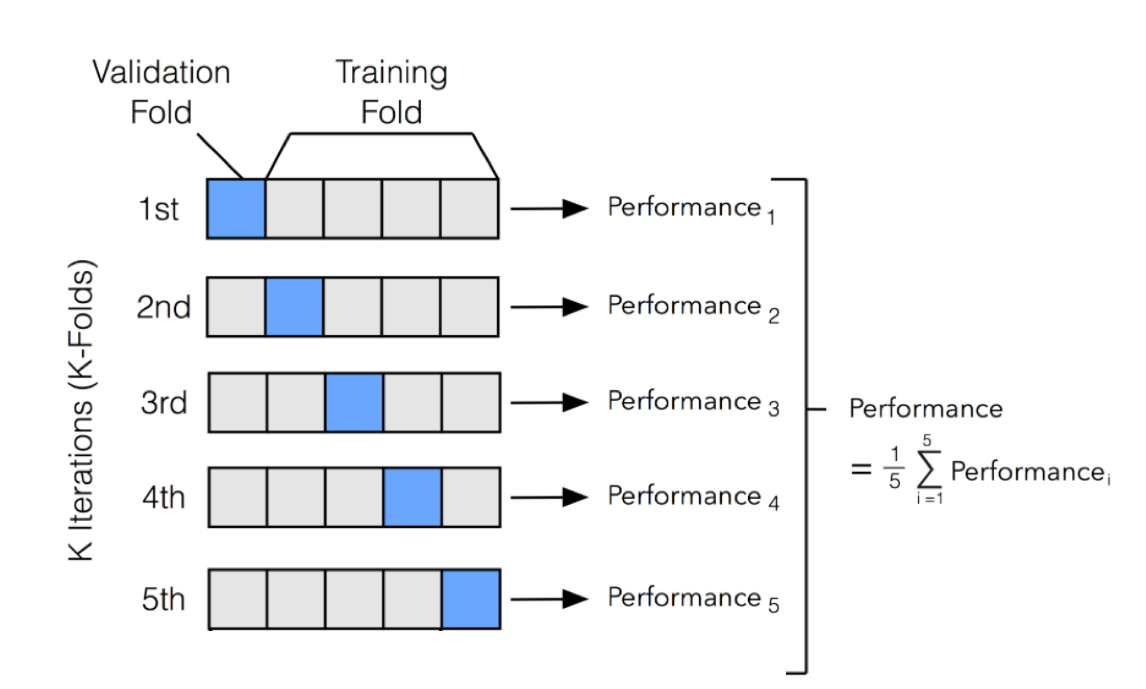
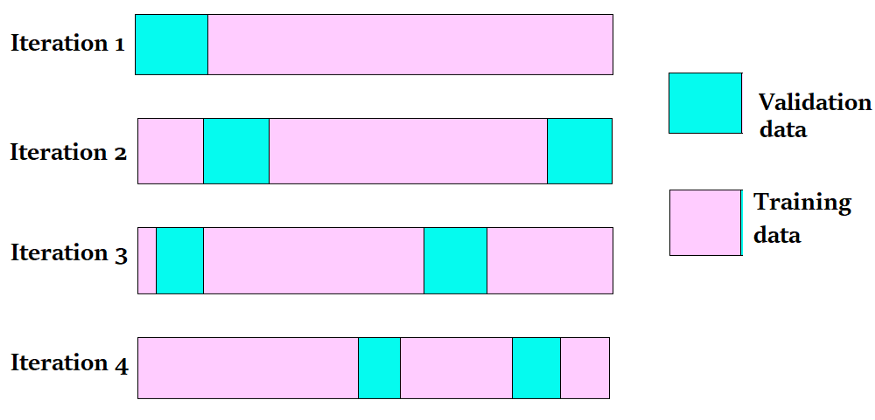
2. K-Fold Cross-Validations
In a Data-Driven World, there is never enough data to train a model; moreover, eliminating a portion of it for validation raises the danger of Underfitting and exposes us to crucial patterns and trends in our data collection, which increases bias. Thus, we seek a strategy that delivers sufficient data for training the model while leaving enough data for validation sets.
K-Fold cross-validation divides the data into k subsets. We may think of it as a holdout technique repeated k times, with one of the k subsets serving as the validation set and the remaining k-1 subsets serving as the training set each time. The error is averaged across all k trials to determine our model’s overall efficiency.
As can be seen, each data point will appear precisely once in a validation set and k-1 times in a training set. This helps us minimize bias since most of the data is utilized for fitting, and variance, as most of the information is also used in the validation set.
Pros
- This will aid in resolving the computing power issue.
- Models may be unaffected by the presence of an outlier in the data.
- It assists us in overcoming the issue of unpredictability.
Cons
- Incorrectly balanced data sets will affect our model.
3. Stratified K-Fold Cross-Validation
The K Fold Cross Validation approach will not operate as predicted for an unbalanced data set. When a data set is unstable, a modest modification to the K Fold cross-validation procedure is required to ensure that each fold has nearly the same number of samples from each output class as the complete. Stratified K Fold Cross Validation involves using a stratum in K Fold Cross-Validation.
Pros
- It may enhance many models through hyper-parameter adjustment.
- Assists us in comparing models.
- It contributes to the reduction of both bias and variance.
Cons
- Execution is expensive.
4. Leave-P-Out Cross-Validation
In this method, we exclude p data points from the training set out of a total of n data points, then train the model using n-p samples and validate using p points. This procedure is performed for all possible combinations, and the error is then averaged.
Pros
- It contains no randomness.
- Bias will be reduced.
Cons
- This is a complete procedure that is computationally infeasible.
Conclusion
In Cross-validations in ML article, we learned about the necessity of validation in the Data Science project life cycle, defined validation and cross-validation, studied the many types of cross-validation approaches, and discussed some of their pros and downsides.
Hope you enjoyed reading this article on cross-validations in ML. Read more blogs here.
The media shown in this article is not owned by Analytics Vidhya and are used at the Author’s discretion.
Currently, I Am pursuing my Bachelors of Technology( B.Tech) from Vellore Institute of Technology. I am very enthusiastic about programming and its real applications including software development, machine learning and data science.
