Picture this, you find yourself in a land of data, where customers roam freely and patterns hide in plain sight. As a brave data scientist, armed with Python as your trusty tool, you embark on a quest to uncover the secrets of customer segmentation. Fear not, for the answer lies in the enchanting realm of hierarchical clustering! In this article, we unravel the mysteries of this magical technique, discovering how it brings order to the chaos of data. Get ready to dive into the Python kingdom, where clusters reign supreme and insights await those who dare to venture into what is hierarchical clustering!
Study Material
- There are multiple ways to perform clustering. I encourage you to check out our awesome guide to the different types of clustering: An Introduction to Clustering and different methods of clustering
- To learn more about clustering and other machine learning algorithms (both supervised and unsupervised) check out the following comprehensive program- Certified AI & ML Blackbelt+ Program
Table of contents
- What is Hierarchical Clustering?
- Types of Hierarchical Clustering
- Supervised vs Unsupervised Learning
- Why Hierarchical Clustering?
- Steps to Perform Hierarchical Clustering
- How to Choose the Number of Clusters in Hierarchical Clustering?
- Solving the Wholesale Customer Segmentation Problem using Hierarchical Clustering
- Conclusion
- Frequently Asked Questions
Quiz Time
Welcome to the quiz on Hierarchical Clustering! Test your knowledge about this clustering technique and its key concepts.
Question
Your answer:
Correct answer:
Your Answers
What is Hierarchical Clustering?
Hierarchical clustering is an unsupervised learning technique used to group similar objects into clusters. It creates a hierarchy of clusters by merging or splitting them based on similarity measures.
Hierarchical clustering groups similar objects into a dendrogram. It merges similar clusters iteratively, starting with each data point as a separate cluster. This creates a tree-like structure that shows the relationships between clusters and their hierarchy.
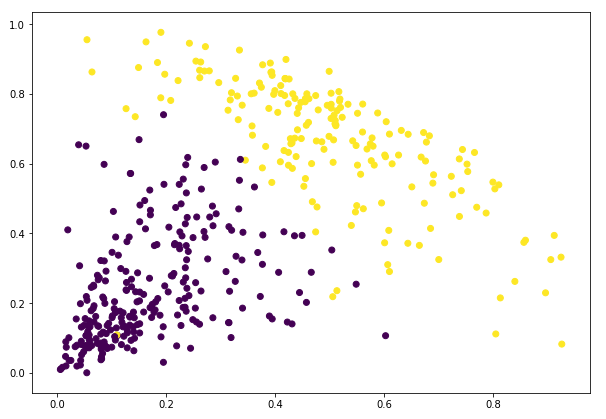
The dendrogram from hierarchical clustering reveals the hierarchy of clusters at different levels, highlighting natural groupings in the data. It provides a visual representation of the relationships between clusters, helping to identify patterns and outliers, making it a useful tool for exploratory data analysis. For example :
Let’s say we have the below points and we want to cluster them into groups:
We can assign each of these points to a separate cluster:
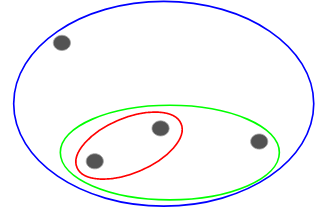
Now, based on the similarity of these clusters, we can combine the most similar clusters together and repeat this process until only a single cluster is left:
We are essentially building a hierarchy of clusters. That’s why this algorithm is called hierarchical clustering. I will discuss how to decide the number of clusters in a later section. For now, let’s look at the different types of hierarchical clustering.
Types of Hierarchical Clustering
There are mainly two types of hierarchical clustering:
- Agglomerative hierarchical clustering
- Divisive Hierarchical clustering
Let’s understand each type in detail.
Agglomerative Hierarchical Clustering
We assign each point to an individual cluster in this technique. Suppose there are 4 data points. We will assign each of these points to a cluster and hence will have 4 clusters in the beginning:
Then, at each iteration, we merge the closest pair of clusters and repeat this step until only a single cluster is left:
We are merging (or adding) the clusters at each step, right? Hence, this type of clustering is also known as additive hierarchical clustering.
Divisive Hierarchical Clustering
Divisive hierarchical clustering works in the opposite way. Instead of starting with n clusters (in case of n observations), we start with a single cluster and assign all the points to that cluster.
So, it doesn’t matter if we have 10 or 1000 data points. All these points will belong to the same cluster at the beginning:
Now, at each iteration, we split the farthest point in the cluster and repeat this process until each cluster only contains a single point:

We are splitting (or dividing) the clusters at each step, hence the name divisive hierarchical clustering.
Agglomerative Clustering is widely used in the industry and that will be the focus in this article. Divisive hierarchical clustering will be a piece of cake once we have handle on the agglomerative type
Supervised vs Unsupervised Learning
It’s important to understand the difference between supervised and unsupervised learning before we dive into hierarchical clustering. Let me explain this difference using a simple example.
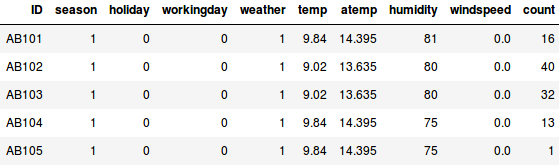
Suppose we want to estimate the count of bikes that will be rented in a city every day:
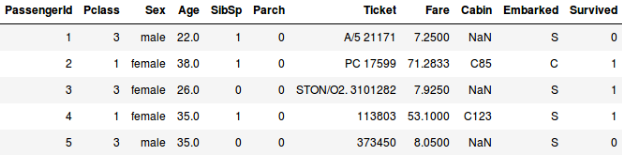
Or, let’s say we want to predict whether a person on board the Titanic survived or not:
Examples
- In the first example, we have to predict the count of bikes based on features like the season, holiday, workingday, weather, temp, etc.
- We are predicting whether a passenger survived or not in the second example. In the ‘Survived’ variable, 0 represents that the person did not survive and 1 means the person did make it out alive. The independent variables here include Pclass, Sex, Age, Fare, etc.
So, when we are given a target variable (count and Survival in the above two cases) which we have to predict based on a given set of predictors or independent variables (season, holiday, Sex, Age, etc.), such problems are called supervised learning problems.
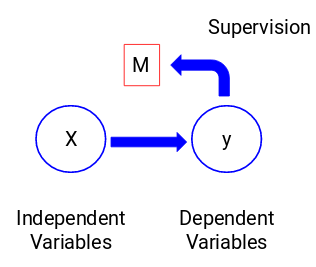
Let’s look at the figure below to understand this visually:
Here, y is our dependent or target variable, and X represents the independent variables. The target variable is dependent on X and hence it is also called a dependent variable. We train our model using the independent variables in the supervision of the target variable and hence the name supervised learning.
Our aim, when training the model, is to generate a function that maps the independent variables to the desired target. Once the model is trained, we can pass new sets of observations and the model will predict the target for them. This, in a nutshell, is supervised learning.
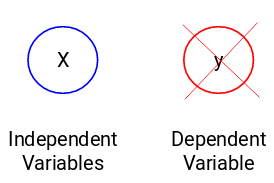
There might be situations when we do not have any target variable to predict. Such problems, without any explicit target variable, are known as unsupervised learning problems. We only have the independent variables and no target/dependent variable in these problems.
We try to divide the entire data into a set of groups in these cases. These groups are known as clusters and the process of making these clusters is known as clustering.
This technique is generally used for clustering a population into different groups. A few common examples include segmenting customers, clustering similar documents together, recommending similar songs or movies, etc.
There are a LOT more applications of unsupervised learning. If you come across any interesting application, feel free to share them in the comments section below!
Now, there are various algorithms that help us to make these clusters. The most commonly used clustering algorithms are K-means and Hierarchical clustering.
Why Hierarchical Clustering?
We should first know how K-means works before we dive into hierarchical clustering. Trust me, it will make the concept of hierarchical clustering all the more easier.
Here’s a brief overview of how K-means works:
- Decide the number of clusters (k)
- Select k random points from the data as centroids
- Assign all the points to the nearest cluster centroid
- Calculate the centroid of newly formed clusters
- Repeat steps 3 and 4
It is an iterative process. It will keep on running until the centroids of newly formed clusters do not change or the maximum number of iterations are reached.
But there are certain challenges with K-means. It always tries to make clusters of the same size. Also, we have to decide the number of clusters at the beginning of the algorithm. Ideally, we would not know how many clusters should we have, in the beginning of the algorithm and hence it a challenge with K-means.
This is a gap hierarchical clustering bridges with aplomb. It takes away the problem of having to pre-define the number of clusters. Sounds like a dream! So, let’s see what hierarchical clustering is and how it improves on K-means.
Let’s understand each type in detail.
Steps to Perform Hierarchical Clustering
We merge the most similar points or clusters in hierarchical clustering – we know this. Now the question is – how do we decide which points are similar and which are not? It’s one of the most important questions in clustering!
Here’s one way to calculate similarity – Take the distance between the centroids of these clusters. The points having the least distance are referred to as similar points and we can merge them. We can refer to this as a distance-based algorithm as well (since we are calculating the distances between the clusters).
In hierarchical clustering, we have a concept called a proximity matrix. This stores the distances between each point. Let’s take an example to understand this matrix as well as the steps to perform hierarchical clustering.
Setting up the Example
Suppose a teacher wants to divide her students into different groups. She has the marks scored by each student in an assignment and based on these marks, she wants to segment them into groups. There’s no fixed target here as to how many groups to have. Since the teacher does not know what type of students should be assigned to which group, it cannot be solved as a supervised learning problem. So, we will try to apply hierarchical clustering here and segment the students into different groups.
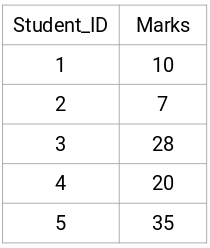
Let’s take a sample of 5 students:
Creating a Proximity Matrix
First, we will create a proximity matrix which will tell us the distance between each of these points. Since we are calculating the distance of each point from each of the other points, we will get a square matrix of shape n X n (where n is the number of observations).
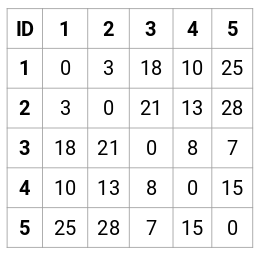
Let’s make the 5 x 5 proximity matrix for our example:
The diagonal elements of this matrix will always be 0 as the distance of a point with itself is always 0. We will use the Euclidean distance formula to calculate the rest of the distances. So, let’s say we want to calculate the distance between point 1 and 2:
√(10-7)^2 = √9 = 3
Similarly, we can calculate all the distances and fill the proximity matrix.
Steps to Perform Hierarchical Clustering
Step 1: First, we assign all the points to an individual cluster:
Different colors here represent different clusters. You can see that we have 5 different clusters for the 5 points in our data.
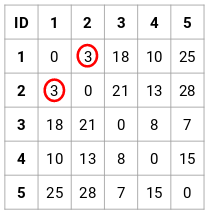
Step 2: Next, we will look at the smallest distance in the proximity matrix and merge the points with the smallest distance. We then update the proximity matrix:
Here, the smallest distance is 3 and hence we will merge point 1 and 2:
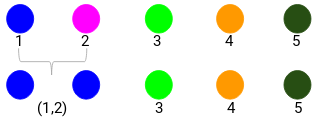
Let’s look at the updated clusters and accordingly update the proximity matrix:
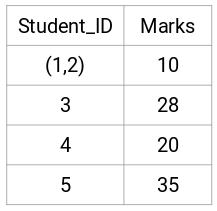
Here, we have taken the maximum of the two marks (7, 10) to replace the marks for this cluster. Instead of the maximum, we can also take the minimum value or the average values as well. Now, we will again calculate the proximity matrix for these clusters:
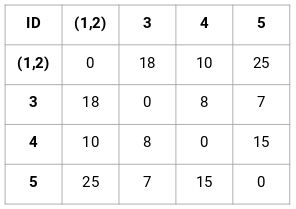
Step 3: We will repeat step 2 until only a single cluster is left.
So, we will first look at the minimum distance in the proximity matrix and then merge the closest pair of clusters. We will get the merged clusters as shown below after repeating these steps:
We started with 5 clusters and finally have a single cluster. This is how agglomerative hierarchical clustering works. But the burning question still remains – how do we decide the number of clusters? Let’s understand that in the next section.
How to Choose the Number of Clusters in Hierarchical Clustering?
Ready to finally answer this question that’s been hanging around since we started learning? To get the number of clusters for hierarchical clustering, we make use of an awesome concept called a Dendrogram.
A dendrogram is a tree-like diagram that records the sequences of merges or splits.
Example
Let’s get back to teacher-student example. Whenever we merge two clusters, a dendrogram will record the distance between these clusters and represent it in graph form. Let’s see how a dendrogram looks:
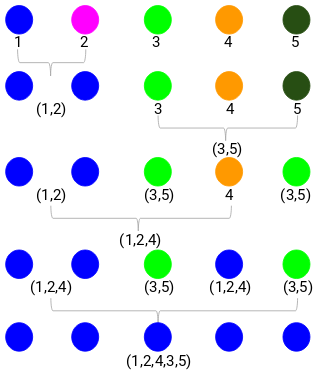
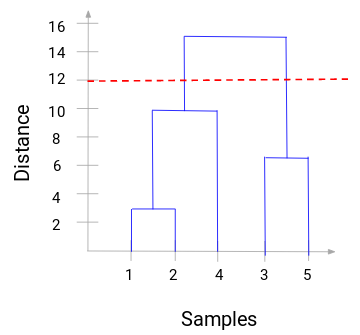
We have the samples of the dataset on the x-axis and the distance on the y-axis. Whenever two clusters are merged, we will join them in this dendrogram and the height of the join will be the distance between these points. Let’s build the dendrogram for our example:
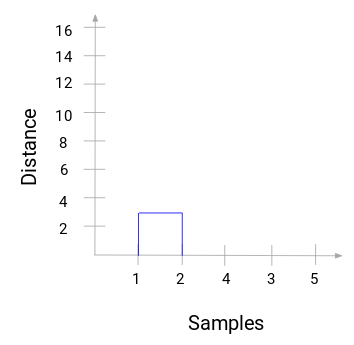
Take a moment to process the above image. We started by merging sample 1 and 2 and the distance between these two samples was 3 (refer to the first proximity matrix in the previous section). Let’s plot this in the dendrogram:
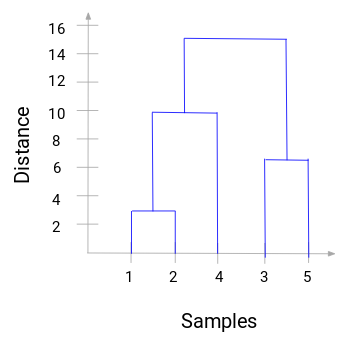
Here, we can see that we have merged sample 1 and 2. The vertical line represents the distance between these samples. Similarly, we plot all the steps where we merged the clusters and finally, we get a dendrogram like this:
We can visualize the steps of hierarchical clustering. More the distance of the vertical lines in the dendrogram, more the distance between those clusters.
Now, we can set a threshold distance and draw a horizontal line (Generally, we try to set the threshold so that it cuts the tallest vertical line). Let’s set this threshold as 12 and draw a horizontal line:
The number of clusters will be the number of vertical lines intersected by the line drawn using the threshold. In the above example, since the red line intersects 2 vertical lines, we will have 2 clusters. One cluster will have a sample (1,2,4) and the other will have a sample (3,5).
This is how we can decide the number of clusters using a dendrogram in Hierarchical Clustering. In the next section, we will implement hierarchical clustering to help you understand all the concepts we have learned in this article.
Solving the Wholesale Customer Segmentation Problem using Hierarchical Clustering
Time to get our hands dirty in Python!
We will be working on a wholesale customer segmentation problem. You can download the dataset using this link. The data is hosted on the UCI Machine Learning repository. The aim of this problem is to segment the clients of a wholesale distributor based on their annual spending on diverse product categories, like milk, grocery, region, etc.
Let’s explore the data first and then apply Hierarchical Clustering to segment the clients.
Required Libraries
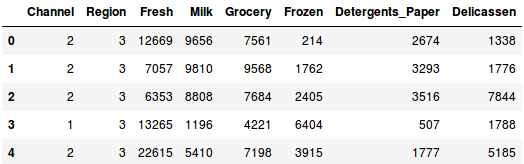
Load the data and look at the first few rows:
Python Code
There are multiple product categories – Fresh, Milk, Grocery, etc. The values represent the number of units purchased by each client for each product. Our aim is to make clusters from this data that can segment similar clients together. We will, of course, use Hierarchical Clustering for this problem.
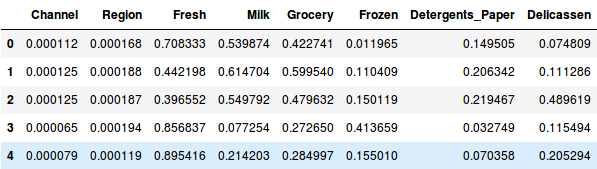
But before applying Hierarchical Clustering, we have to normalize the data so that the scale of each variable is the same. Why is this important? Well, if the scale of the variables is not the same, the model might become biased towards the variables with a higher magnitude like Fresh or Milk (refer to the above table).
So, let’s first normalize the data and bring all the variables to the same scale:
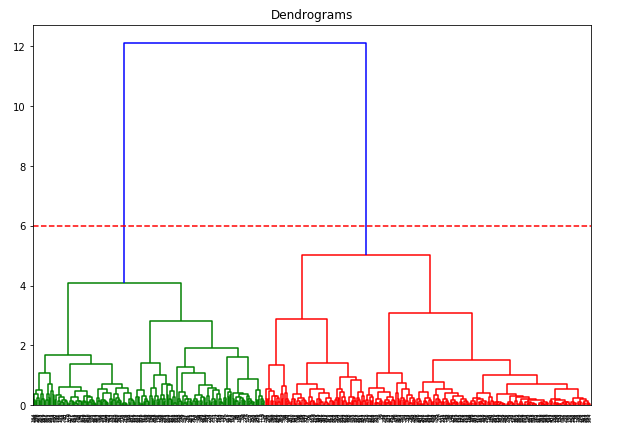
Here, we can see that the scale of all the variables is almost similar. Now, we are good to go. Let’s first draw the dendrogram to help us decide the number of clusters for this particular problem:
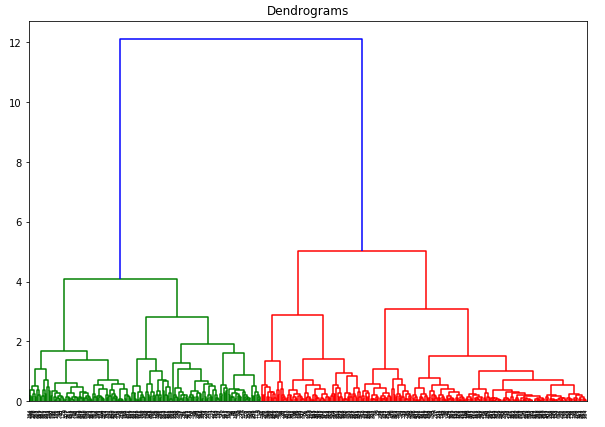
The x-axis contains the samples and y-axis represents the distance between these samples. The vertical line with maximum distance is the blue line and hence we can decide a threshold of 6 and cut the dendrogram:
We have two clusters as this line cuts the dendrogram at two points. Let’s now apply hierarchical clustering for 2 clusters:
We can see the values of 0s and 1s in the output since we defined 2 clusters. 0 represents the points that belong to the first cluster and 1 represents points in the second cluster. Let’s now visualize the two clusters:
Awesome! We can clearly visualize the two clusters here. This is how we can implement hierarchical clustering in Python.
Conclusion
Hierarchical clustering is a super useful way of segmenting observations. The advantage of not having to pre-define the number of clusters gives it quite an edge over k-Means.
If you are still relatively new to data science, I highly recommend taking the Applied Machine Learning course. It is one of the most comprehensive end-to-end machine learning courses you will find anywhere. Hierarchical clustering is just one of a diverse range of topics we cover in the course.
What are your thoughts on hierarchical clustering? Do you feel there’s a better way to create clusters using less computational resources? Connect with me in the comments section below and let’s discuss!
Frequently Asked Questions
A. Hierarchical agglomerative clustering (HAC) merges the most similar clusters together, starting with each data point as a separate cluster. HAC can be used to identify natural groupings in data and is often used in exploratory data analysis and machine learning tasks such as image segmentation and document clustering.
A. A dendrogram clustering is a tree-like diagram that displays the hierarchical relationships between clusters in a clustering analysis. It is a useful tool for identifying natural groupings or structures present in the data and for identifying similarities, differences, and outliers between clusters.
A. An example of a hierarchical cluster is a dendrogram that shows the hierarchical relationships between different species based on their genetic similarities.
A. Hierarchical clustering is used in various fields such as biology, sociology, marketing, and computer science. It is commonly applied in biological taxonomy, customer segmentation, pattern recognition, and image analysis.
A. In hierarchical clustering, we use distance metrics to assess how similar or different two clusters are. One common metric is Euclidean distance, which measures the straight-line distance between two points. Think of it as the shortest path between them. Another metric is Manhattan distance, which looks at the ‘horizontal’ and ‘vertical’ steps needed to get from one point to another, like moving in a grid.
So, in simple terms, we’re basically measuring how near or far these clusters are from each other. This helps the clustering process decide which clusters should be grouped together. Hope that clarifies it!