This article was published as a part of the Data Science Blogathon.
Introduction
In this article, we will first discuss some of the common methods of Ensemble and their disadvantages. Then we will discuss how those disadvantages can be taken care of by another way of Ensemble known as Stacking and Blending and how to build it in python. Finally, we will wrap everything and create an easy-to-use function.
Common Ensemble Methods and their Disadvantages
Ensemble methods are a machine learning technique that combines different models to make an optimum model. Different machine learning models can extract patterns in different ways, by using all of them a better model can be made. One of the common methods is –
- Building different models and taking mean or a majority vote of them
Though this method is very much simple to use and often gives a better result the problem is the weaker models get equal priority as the stronger models which might result in a decrease in a score sometimes.
- Building different models and taking a weighted average of them
In this method, we can assign higher weightage to the stronger models but it is difficult to assume the weights which is also not that much desirable.
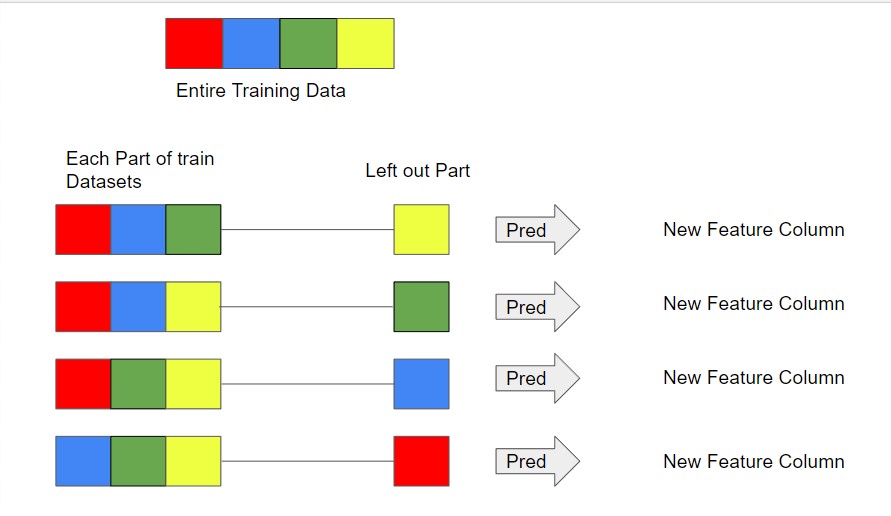
Stacking and Blending: To get rid of the above-mentioned problems stacking and blending can be used for Ensemble Modelling. The steps are –
- Divide the training data into equal N parts.
- By Keeping one part of the data aside build the training datasets of N Data Frames.
- Take each of the training data and make a prediction on its left-out part.
- Take the entire training data to predict by the same methods on the testing data.
- Now we have predictions on each part of the training data and the testing data.
- Repeat the same process with other methods.
- Use these new predictions as features to build a new set of training and testing data.
- Make the final prediction on the new testing data with the help of new training data.
Regression by Stacking and Blending in Python
import pandas as pd
import numpy as np
x_train = pd.read_csv("C:\Users\chakr\Desktop\Clean_data\X_train_reg.csv")
y_train = pd.read_csv("C:\Users\chakr\Desktop\Clean_data\y_train_reg.csv")
x_train.head()
from sklearn.model_selection import train_test_split x_train1, x_train2, y_train1, y_train2 = train_test_split( x_train, y_train, test_size=0.25, random_state=42)
Step 1: Divide the Datasets into N parts ( here we use 20 Parts)
def get_dataset(x_train,y_train,N=5) :
merge = pd.concat([x_train,y_train],axis=1)
merge = merge.sample(frac=1, random_state=1).reset_index(drop=True)
y_train = merge.iloc[:,(merge.shape[1]-1):(merge.shape[1])]
x_train = merge.iloc[:,0:(merge.shape[1]-1)]
z = int(len(x_train)/N)
start = [0]
stop = []
for i in range(1,N):
start.append(z*i)
stop.append(z*i)
stop.append(len(x_train))
c = list()
train_data = list()
test_data = list()
y_data = list()
for i in range(0,N):
c=list(range(start[i],stop[i]))
train_data.append(x_train.iloc[[k for k in range(0,len(x_train)) if k not in c],:])
y_data.append(y_train.iloc[[k for k in range(0,len(y_train)) if k not in c],:])
test_data.append(x_train.iloc[c,:])
return(train_data,y_data,test_data,y_train)
datasets = get_dataset(x_train1,y_train1,20)
train_data = datasets[0]
y_data = datasets[1]
test_data = datasets[2]
final_y = datasets[3]
Now we have the following datasets.
- train_data: 20 sets of training data leaving each part out one at a time.
- y_data: Target column of each of the sets of training data.
- test_data: The remaining part of each of the training datasets
- final_y: Target column of the entire training data.
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from catboost import CatBoostRegressor, Pool
models = [LinearRegression(),
DecisionTreeRegressor(),
KNeighborsRegressor(),
CatBoostRegressor(logging_level ='Silent')]
code = ['lin_reg','dtree_reg','Knn_reg','cat_reg']
Step 3: Prediction function for all the models together
def stack(x_train, y_train , x_test , models,code):
def flatten_list(_2d_list):
flat_list = []
for element in _2d_list:
if type(element) is list:
for item in element:
flat_list.append(item)
else:
flat_list.append(element)
return flat_list
result = list()
for i in list(range(len(models))):
reg = models[i]
reg.fit(x_train,y_train)
test_pred = flatten_list(reg.predict(x_test).tolist())
result.append(test_pred)
result_df = pd.DataFrame()
for i in list(range(len(code))):
result_df[code[i]] = result[i]
return result_df
Step 4: Predict for each the chunks to get the final Data Frame
final_df = pd.DataFrame(columns = code)
for i in range(0,len(train_data)):
current_df = stack(train_data[i],y_data[i],test_data[i],models,code)
final_df = pd.concat([final_df,current_df])
final_test = stack(x_train1,y_train1,x_train2,models,code)
final_df.head()
Step 5: Build the second Layer Model
reg2 = CatBoostRegressor(logging_level ='Silent') reg2.fit(final_df,final_y) test_pred = reg2.predict(final_test) mean_squared_error(test_pred,y_train2)**0.5
 Wrap everything in a function
Wrap everything in a function
In the above section, we saw how the stacking and blending are working to help us build an ensemble model. In this section, we will wrap everything up to build a useful function that can return prediction directly.
def stackblend_reg(x_train,y_train,x_test,models,code,N=20,final_layer=LinearRegression()):
def get_dataset(x_train,y_train,N=5) :
merge = pd.concat([x_train,y_train],axis=1)
merge = merge.sample(frac=1, random_state=1).reset_index(drop=True)
y_train = merge.iloc[:,(merge.shape[1]-1):(merge.shape[1])]
x_train = merge.iloc[:,0:(merge.shape[1]-1)]
z = int(len(x_train)/N)
start = [0]
stop = []
for i in range(1,N):
start.append(z*i)
stop.append(z*i)
stop.append(len(x_train))
c = list()
train_data = list()
test_data = list()
y_data = list()
for i in range(0,N):
c=list(range(start[i],stop[i]))
train_data.append(x_train.iloc[[k for k in range(0,len(x_train)) if k not in c],:])
y_data.append(y_train.iloc[[k for k in range(0,len(y_train)) if k not in c],:])
test_data.append(x_train.iloc[c,:])
return(train_data,y_data,test_data,y_train)
datasets = get_dataset(x_train,y_train,N)
train_data = datasets[0]
y_data = datasets[1]
test_data = datasets[2]
final_y = datasets[3]
def stack(x_train, y_train , x_test , models=models,code=code):
def flatten_list(_2d_list):
flat_list = []
for element in _2d_list:
if type(element) is list:
for item in element:
flat_list.append(item)
else:
flat_list.append(element)
return flat_list
result = list()
for i in list(range(len(models))):
reg = models[i]
reg.fit(x_train,y_train)
test_pred = flatten_list(reg.predict(x_test).tolist())
result.append(test_pred)
result_df = pd.DataFrame()
for i in list(range(len(code))):
result_df[code[i]] = result[i]
return result_df
final_df = pd.DataFrame(columns = code)
for i in range(0,len(train_data)):
current_df = stack(train_data[i],y_data[i],test_data[i],models,code)
final_df = pd.concat([final_df,current_df])
final_test = stack(x_train,y_train,x_test,models,code)
reg2 = final_layer
reg2.fit(final_df,final_y)
test_pred = reg2.predict(final_test)
return test_pred
Use the function to Predict
stack_pred = stackblend_reg(x_train1,y_train1,x_train2,
models = [LinearRegression(),
DecisionTreeRegressor(),
KNeighborsRegressor(),
CatBoostRegressor(logging_level ='Silent')],
code = ['lin_reg','dtree_reg','Knn_reg','cat_reg'],N=20,
final_layer=CatBoostRegressor(logging_level ='Silent'))
mean_squared_error(stack_pred,y_train2)**0.5
Conclusion
Now we have the function to get prediction directly, we can with different types of the final layer model to see what works the best. A similar function can be made for the classification problems too. These functions should be highly time-saving and easy to use during solving Supervised Learning problems.
The media shown in this article is not owned by Analytics Vidhya and is used at the Author’s discretion.




