Heart Disease Prediction using Machine Learning

This article was published as a part of the Data Science Blogathon.

Overview

In this article, we will be closely working with the heart disease prediction and for that, we will be looking into the heart disease dataset from that dataset we will derive various insights that help us know the weightage of each feature and how they are interrelated to each other but this time our sole aim is to detect the probability of person that will be affected by a savior heart problem or not.

Plotting Libraries

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import cufflinks as cf
%matplotlib inline

Metrics for Classification technique

from sklearn.metrics import classification_report,confusion_matrix,accuracy_score

Scaler

from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import  RandomizedSearchCV, train_test_split

Model building

from xgboost import XGBClassifier
from catboost import CatBoostClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC

Data Loading

Here we will be using the pandas read_csv function to read the dataset. Specify the location of the dataset and import them.

Importing Data

data = pd.read_csv("heart.csv")
data.head(6) # Mention no of rows to be displayed from the top in the argument

Output:

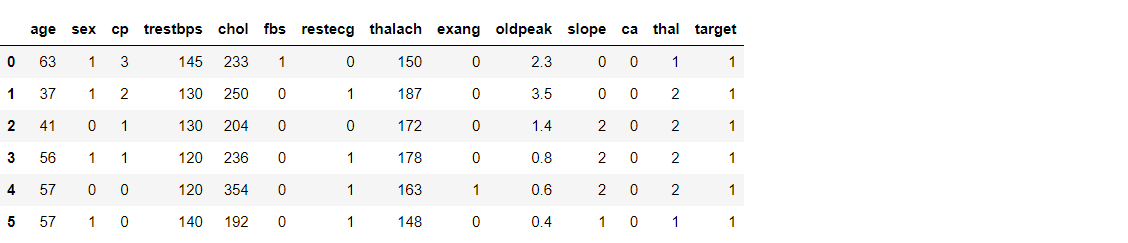
Exploratory Data Analysis

Now, let’s see the size of the dataset

data.shape

Output:

(303, 14)

Inference: We have a dataset with 303 rows which indicates a smaller set of data.

As above we saw the size of our dataset now let’s see the type of each feature that our dataset holds.

Python Code:



Inference: The inference we can derive from the above output is:

• Out of 14 features, we have 13 int types and only one with the float data types.
• Woah! Fortunately, this dataset doesn’t hold any missing values.

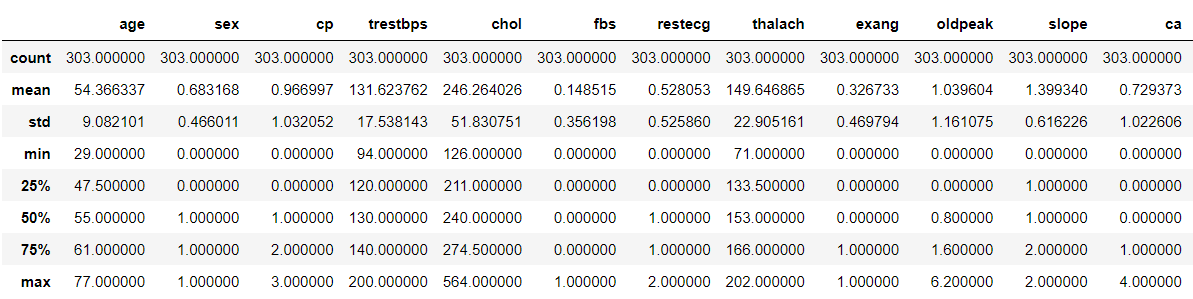
As we are getting some information from each feature so let’s see how statistically the dataset is spread.

data.describe()

Output:

 

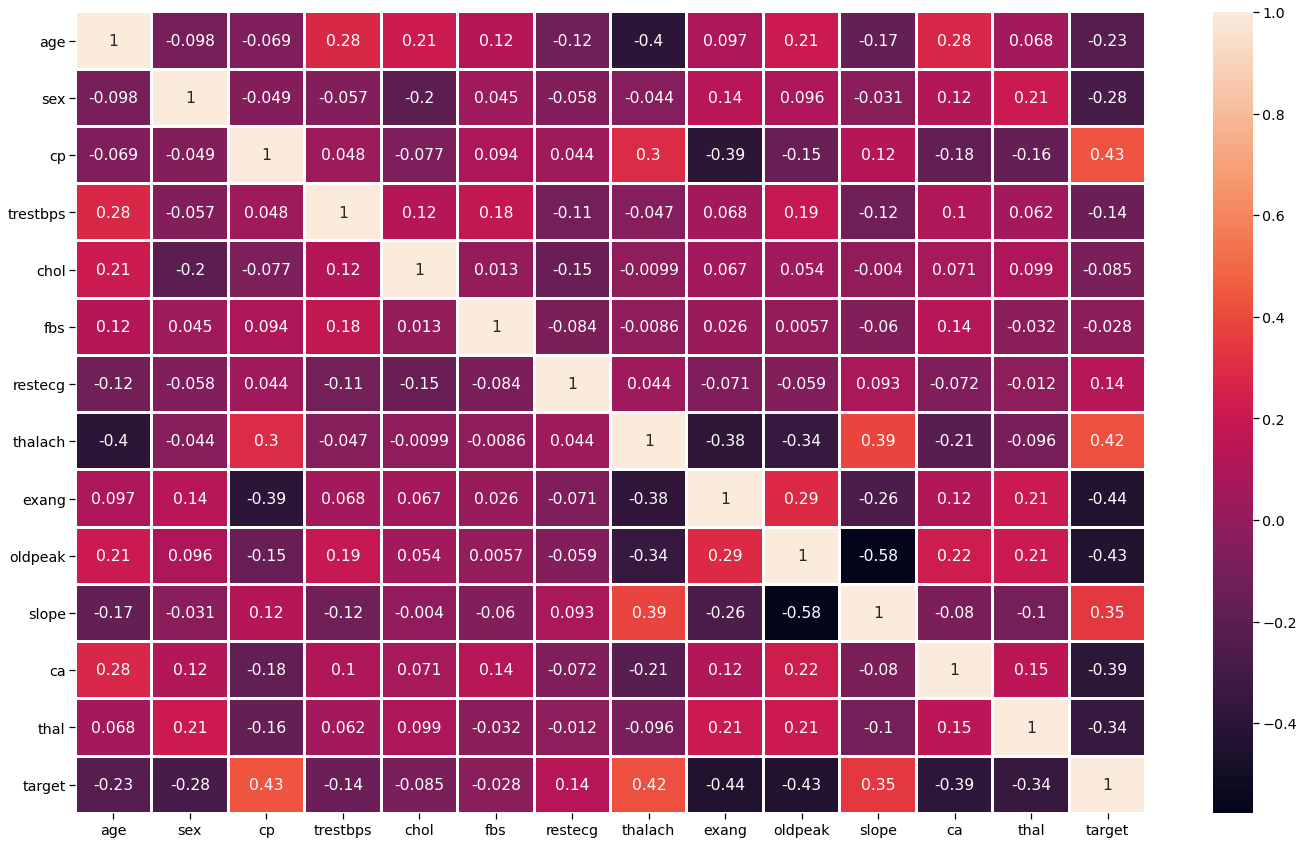
It is always better to check the correlation between the features so that we can analyze that which feature is negatively correlated and which is positively correlated so, Let’s check the correlation between various features.

plt.figure(figsize=(20,12))
sns.set_context('notebook',font_scale = 1.3)
sns.heatmap(data.corr(),annot=True,linewidth =2)
plt.tight_layout()

Output:

 

By far we have checked the correlation between the features but it is also a good practice to check the correlation of the target variable.

So, let’s do this!

sns.set_context('notebook',font_scale = 2.3)
data.drop('target', axis=1).corrwith(data.target).plot(kind='bar', grid=True, figsize=(20, 10), 
                                                        title="Correlation with the target feature")
plt.tight_layout()

Output:

 

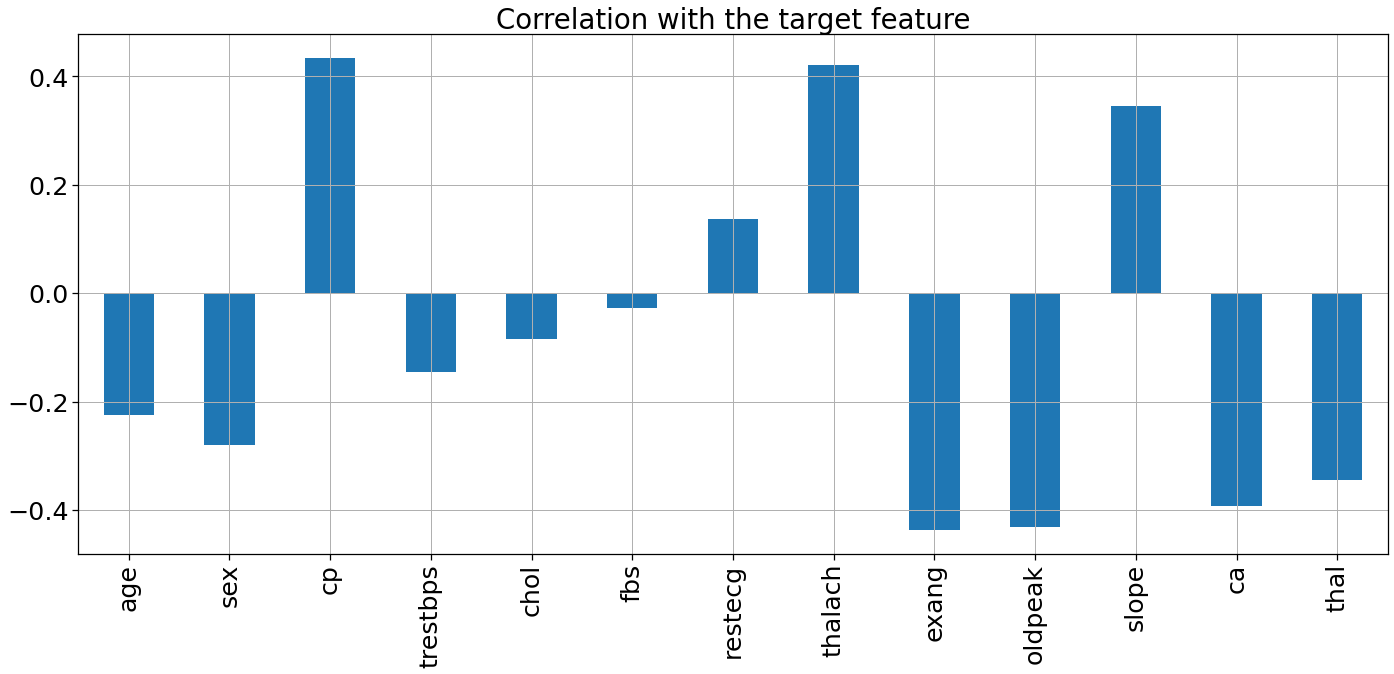
Inference: Insights from the above graph are:

• Four feature( “cp”, “restecg”, “thalach”, “slope” ) are positively correlated with the target feature.
• Other features are negatively correlated with the target feature.

So, we have done enough collective analysis now let’s go for the analysis of the individual features which comprises both univariate and bivariate analysis.

Age(“age”) Analysis

Here we will be checking the 10 ages and their counts.

plt.figure(figsize=(25,12))
sns.set_context('notebook',font_scale = 1.5)
sns.barplot(x=data.age.value_counts()[:10].index,y=data.age.value_counts()[:10].values)
plt.tight_layout()

Output:

 

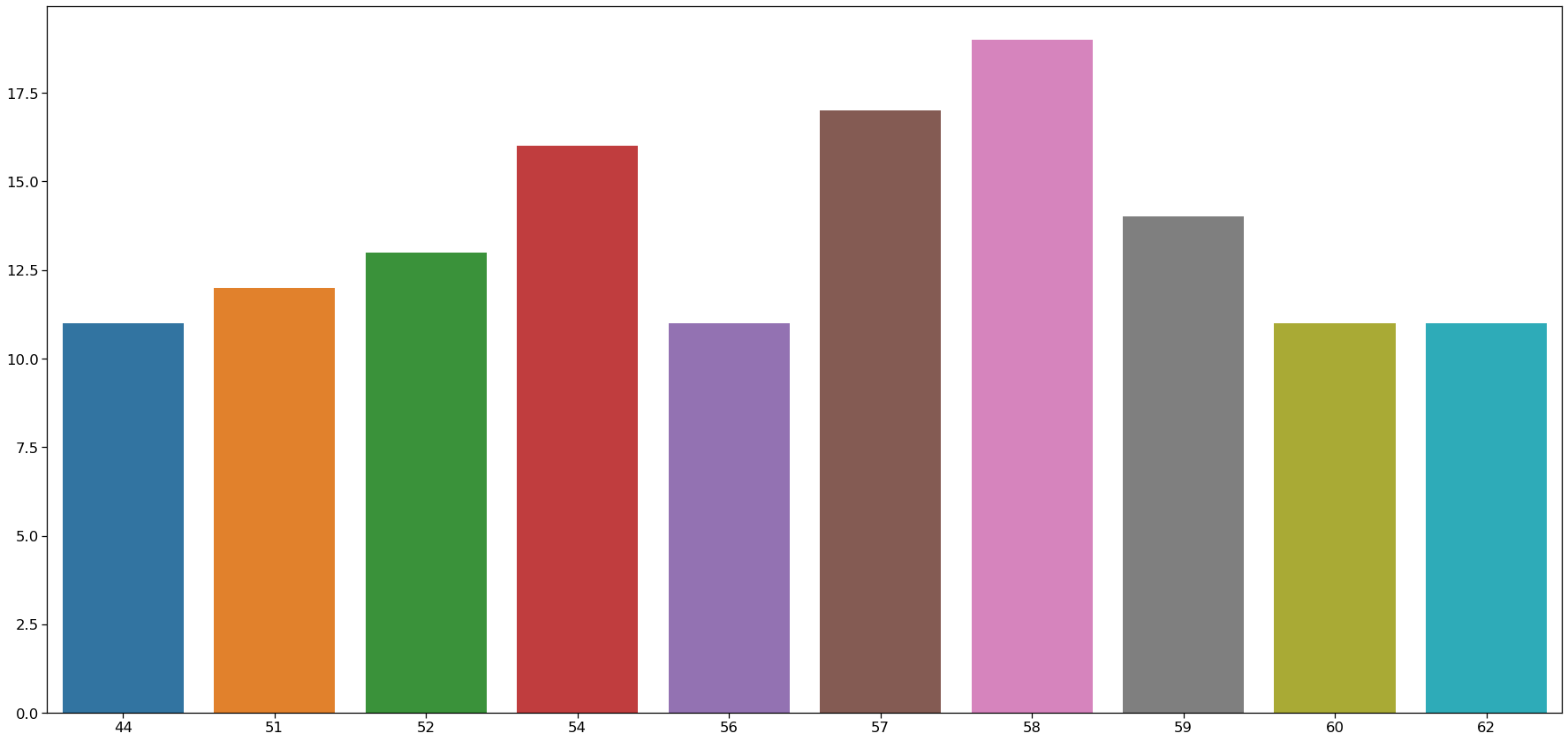
Inference:  Here we can see that the 58 age column has the highest frequency.

Let’s check the range of age in the dataset.

minAge=min(data.age)
maxAge=max(data.age)
meanAge=data.age.mean()
print('Min Age :',minAge)
print('Max Age :',maxAge)
print('Mean Age :',meanAge)

Output:

Min Age : 29 Max Age : 77 Mean Age : 54.366336633663366

We should divide the Age feature into three parts – “Young”, “Middle” and “Elder”

Young = data[(data.age>=29)&(data.age<40)]
Middle = data[(data.age>=40)&(data.age<55)]
Elder = data[(data.age>55)]

plt.figure(figsize=(23,10))
sns.set_context('notebook',font_scale = 1.5)
sns.barplot(x=['young ages','middle ages','elderly ages'],y=[len(Young),len(Middle),len(Elder)])
plt.tight_layout()

Output:

 

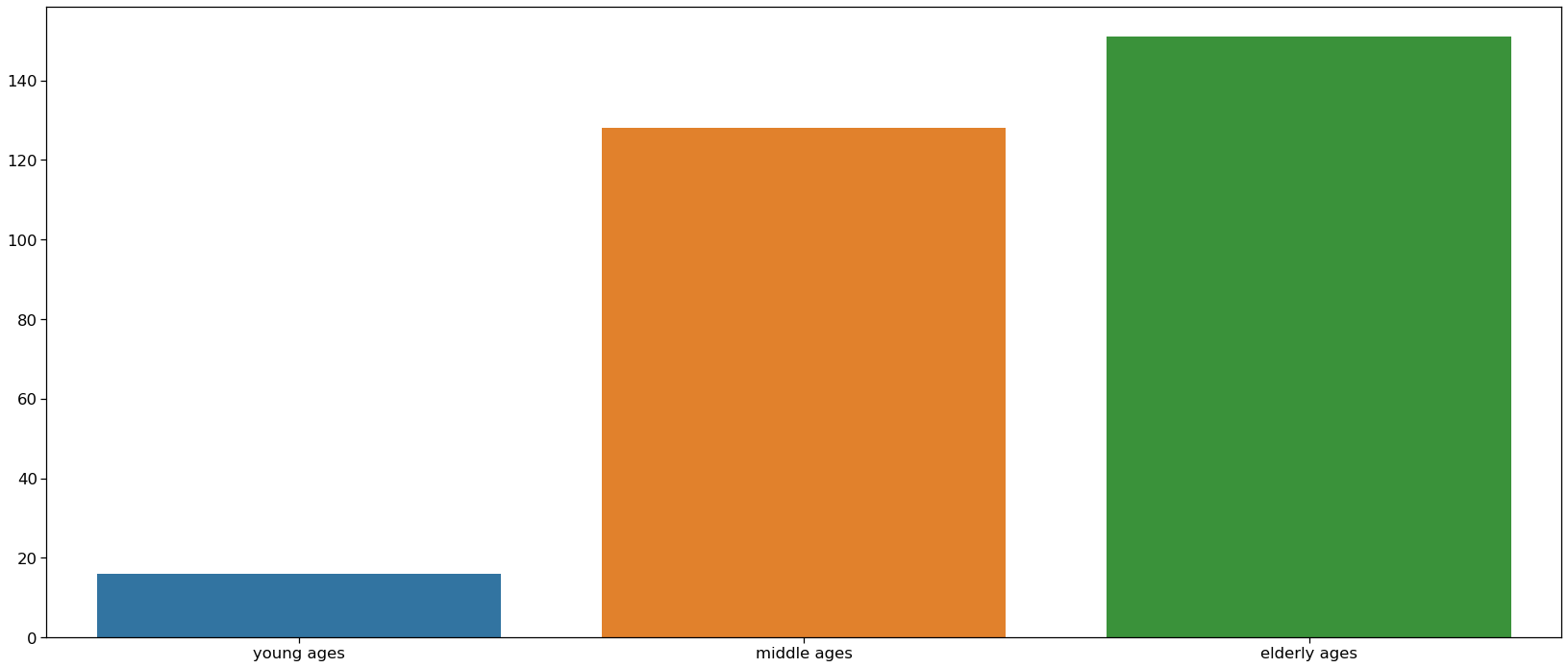
Inference: Here we can see that elder people are the most affected by heart disease and young ones are the least affected.

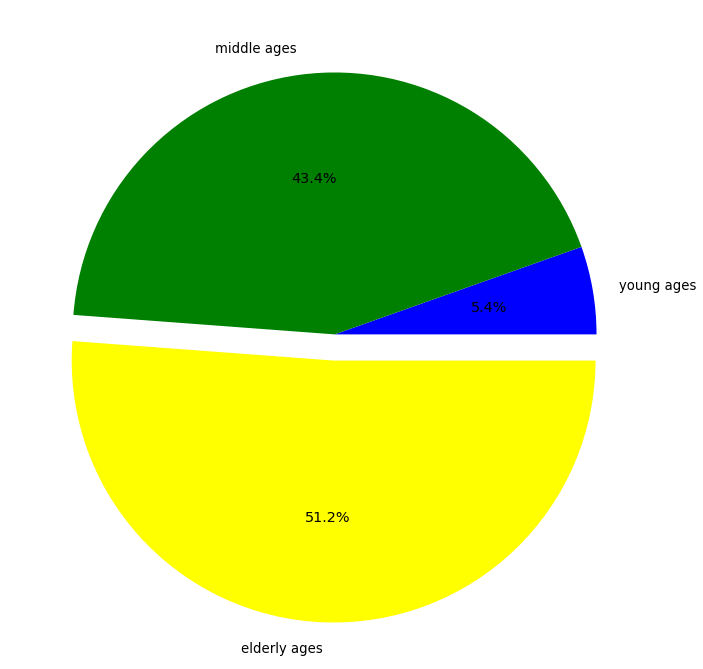
To prove the above inference we will plot the pie chart.

colors = ['blue','green','yellow']
explode = [0,0,0.1]
plt.figure(figsize=(10,10))
sns.set_context('notebook',font_scale = 1.2)
plt.pie([len(Young),len(Middle),len(Elder)],labels=['young ages','middle ages','elderly ages'],explode=explode,colors=colors, autopct='%1.1f%%')
plt.tight_layout()

Output:

 

Sex(“sex”) Feature Analysis

plt.figure(figsize=(18,9))
sns.set_context('notebook',font_scale = 1.5)
sns.countplot(data['sex'])
plt.tight_layout()

Output:

 

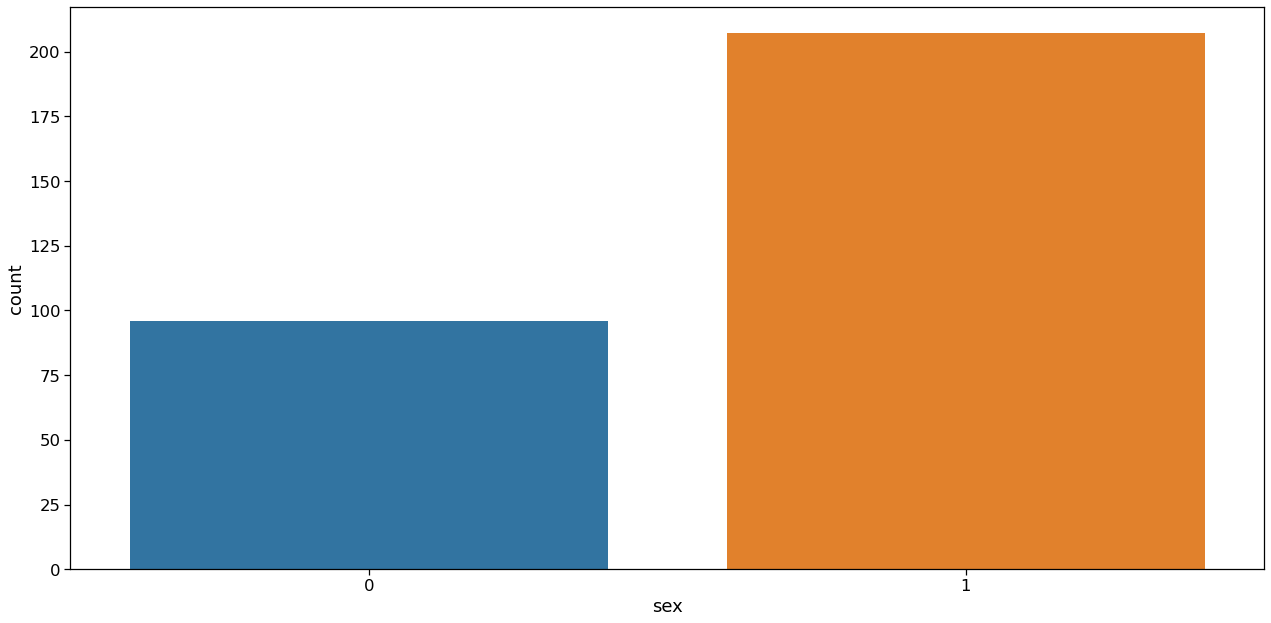
Inference: Here it is clearly visible that, Ratio of Male to Female is approx 2:1.

Now let’s plot the relation between sex and slope.

plt.figure(figsize=(18,9))
sns.set_context('notebook',font_scale = 1.5)
sns.countplot(data['sex'],hue=data["slope"])
plt.tight_layout()

Output:

 

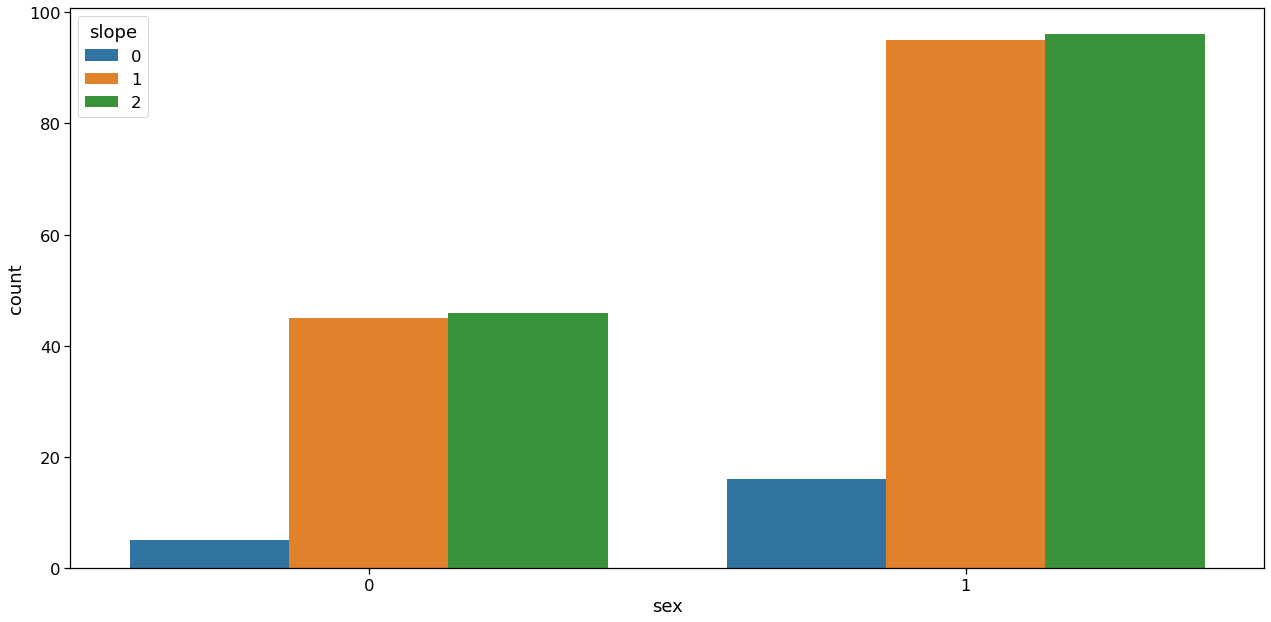
Inference: Here it is clearly visible that the slope value is higher in the case of males(1).

Chest Pain Type(“cp”) Analysis

plt.figure(figsize=(18,9))
sns.set_context('notebook',font_scale = 1.5)
sns.countplot(data['cp'])
plt.tight_layout()

Output:

 

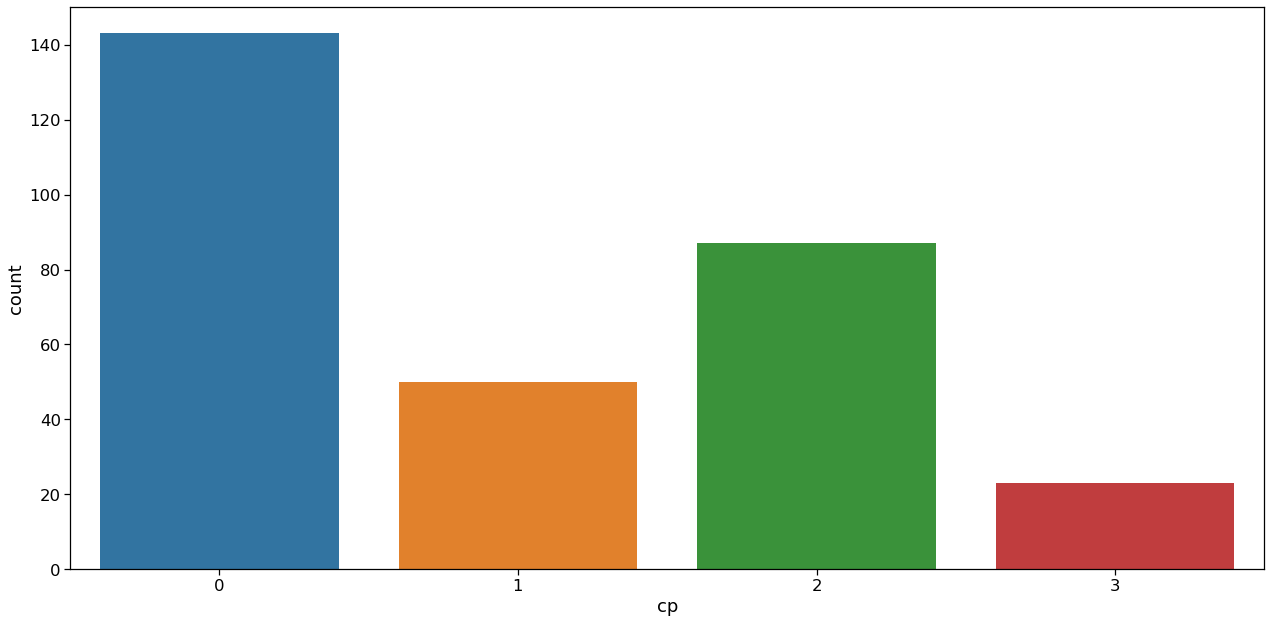
Inference: As seen, there are 4 types of chest pain

1. status at least
2. condition slightly distressed
3. condition medium problem
4. condition too bad

Analyzing cp vs target column

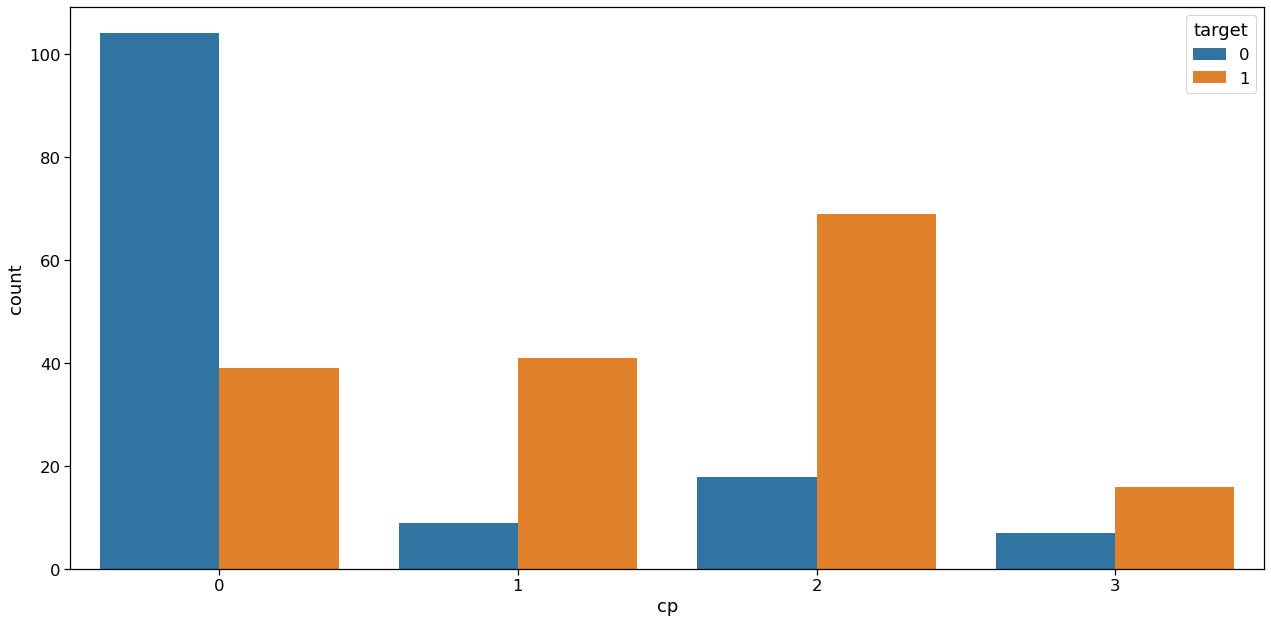
Inference: From the above graph we can make some inferences,

• People having the least chest pain are not likely to have heart disease.
• People having severe chest pain are likely to have heart disease.

Elderly people are more likely to have chest pain.

Thal Analysis

plt.figure(figsize=(18,9))
sns.set_context('notebook',font_scale = 1.5)
sns.countplot(data['thal'])
plt.tight_layout()

Output:

 

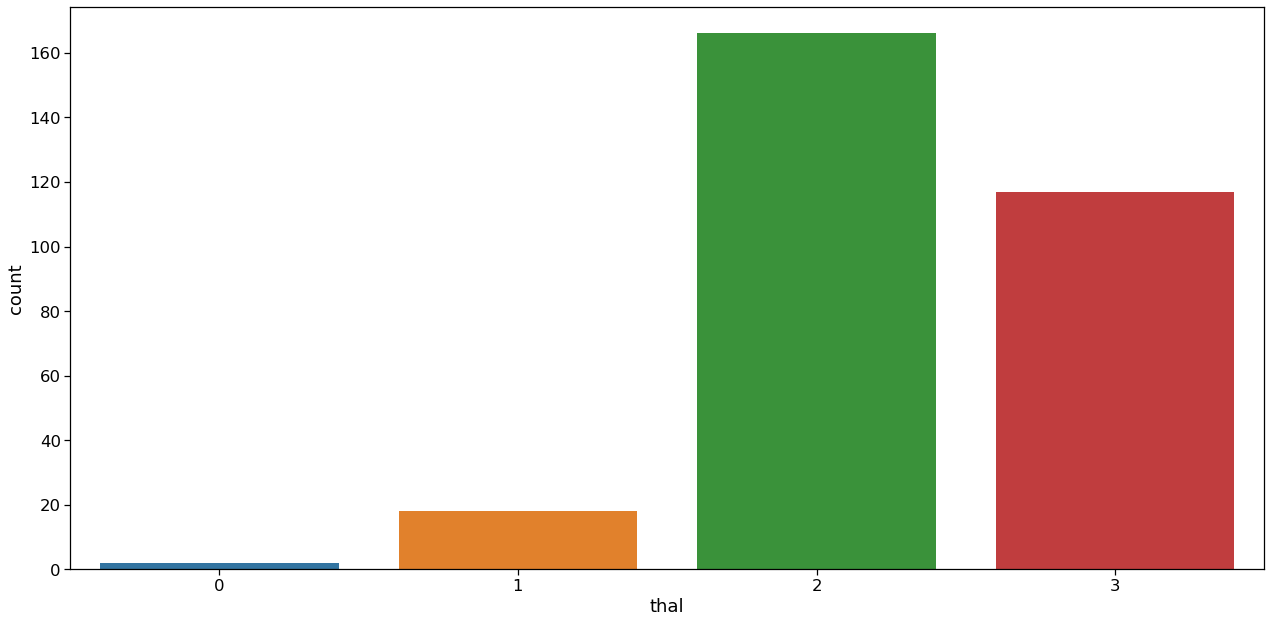
Target

plt.figure(figsize=(18,9))
sns.set_context('notebook',font_scale = 1.5)
sns.countplot(data['target'])
plt.tight_layout()

Output:

 

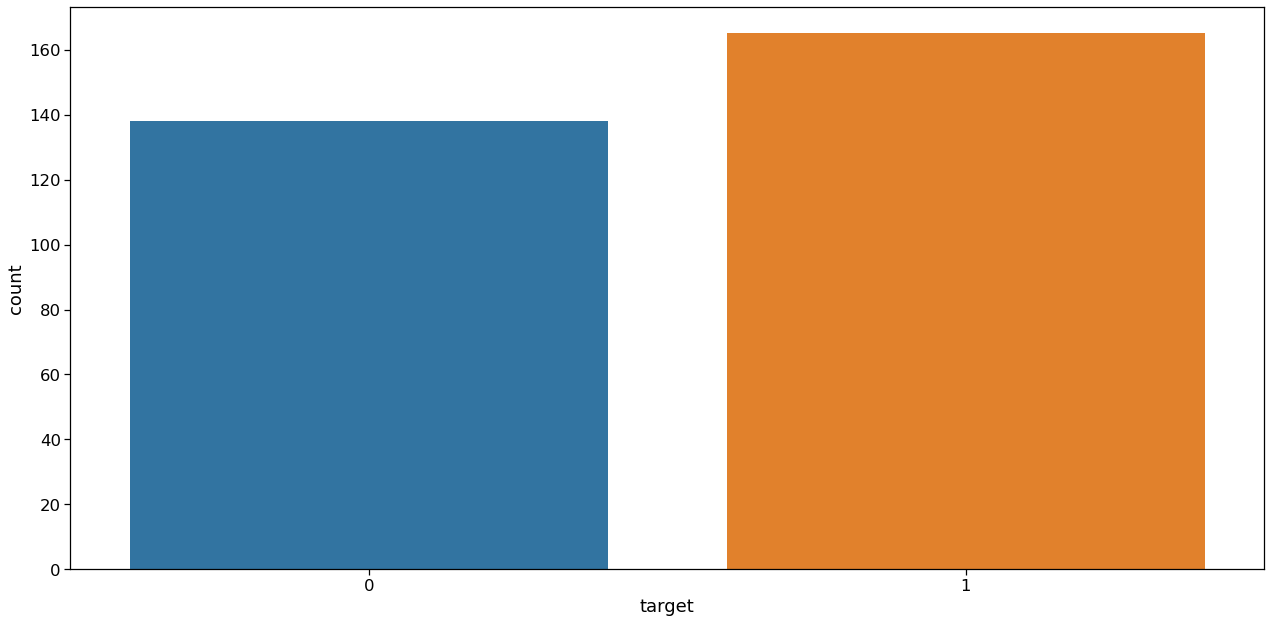
Inference: The ratio between 1 and 0 is much less than 1.5 which indicates that the target feature is not imbalanced. So for a balanced dataset, we can use accuracy_score as evaluation metrics for our model.

Feature Engineering

Now we will see the complete description of the continuous data as well as the categorical data

categorical_val = []
continous_val = []
for column in data.columns:
    print("--------------------")
    print(f"{column} : {data[column].unique()}")
    if len(data[column].unique()) <= 10:
        categorical_val.append(column)
    else:
        continous_val.append(column)

Output:

 

Now here first we will be removing the target column from our set of features then we will categorize all the categorical variables using the get dummies method which will create a separate column for each category suppose X variable contains 2 types of unique values then it will create 2 different columns for the X variable.

categorical_val.remove('target')
dfs = pd.get_dummies(data, columns = categorical_val)
dfs.head(6)

Output:

 

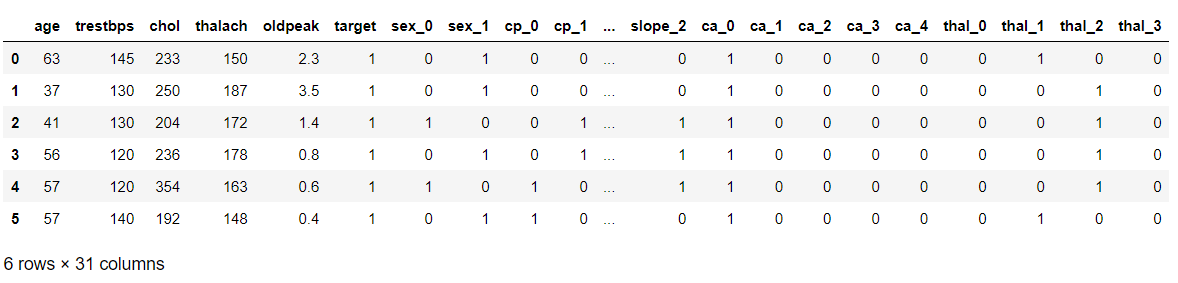
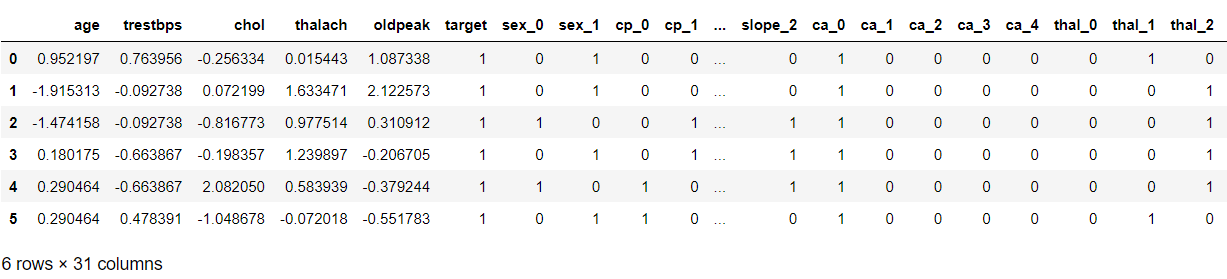
Now we will be using the standard scaler method to scale down the data so that it won’t raise the outliers also dataset which is scaled to general units leads to having better accuracy.

sc = StandardScaler()
col_to_scale = ['age', 'trestbps', 'chol', 'thalach', 'oldpeak']
dfs[col_to_scale] = sc.fit_transform(dfs[col_to_scale])
dfs.head(6)

Output:

 

Modeling

Splitting our Dataset

X = dfs.drop('target', axis=1)
y = dfs.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

The KNN Machine Learning Algorithm

knn = KNeighborsClassifier(n_neighbors = 10)
knn.fit(X_train,y_train)
y_pred1 = knn.predict(X_test)
print(accuracy_score(y_test,y_pred1))

Output:

0.8571428571428571

Conclusion on Heart Disease Prediction

1. We did data visualization and data analysis of the target variable, age features, and whatnot along with its univariate analysis and bivariate analysis.

2. We also did a complete feature engineering part in this article which summons all the valid steps needed for further steps i.e.
model building.

3. From the above model accuracy, KNN is giving us the accuracy which is 89%.

Endnotes

Here’s the repo link to this article. Hope you liked my article on Heart disease detection using ML. If you have any opinions or questions, then comment below.

Read on AV Blog about various predictions using Machine Learning.

About Me

Greeting to everyone, I’m currently working in TCS and previously, I worked as a Data Science Analyst in Zorba Consulting India. Along with full-time work, I’ve got an immense interest in the same field, i.e. Data Science, along with its other subsets of Artificial Intelligence such as Computer Vision, Machine Learning, and Deep learning; feel free to collaborate with me on any project on the domains mentioned above (LinkedIn).

Hope you liked my article on Heart Disease Prediction? You can access my other articles, which are published on Analytics Vidhya as a part of the Blogathon link.

The media shown in this article is not owned by Analytics Vidhya and are used at the Author’s discretion.