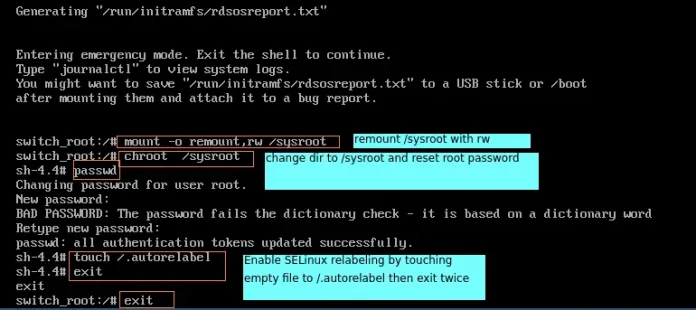
Given an integer N, the task is to paint a grid of size N x 3 using colors Red, Yellow, or Green while making such that no pair of adjacent cells has the same color. Print the number of distinct ways in which it is possible
Examples:
Input: N = 1
Output: 12
Explanation:
Following 12 possible ways to paint the grid exists:
- Red, Yellow, Red
- Yellow, Red, Yellow
- Green, Red, Yellow
- Red, Yellow, Green
- Yellow, Red, Green
- Green, Red, Green
- Red, Green, Red
- Yellow, Green, Red
- Green, Yellow, Red
- Red, Green, Yellow
- Yellow, Green, Yellow
- Green, Yellow, Green
Input: N = 2
Output: 102
Approach: Follow the steps below to solve the problem:
- Ways to color a row can be split into the following two categories:
- The leftmost and rightmost cells are of the same color.
- The leftmost and rightmost cells are of different colors.
- Considering the first case:
- Six possible ways exist to paint the row such that the leftmost and rightmost colors are of the same.
- For every color occupying both the leftmost and rightmost cell, there exists two different colors with which the middle row can be colored.
- Considering the second case:
- Six possible ways exist to paint the leftmost and rightmost colors are different.
- Three choices for the left cell, two choices for the middle, and fill the rightmost cell with the only remaining color. Therefore, the total number of possibilities is 3*2*1 = 6.
- Now, for the subsequent cells, look at the following example:
- If the previous row is painted as Red Green Red, then there are the following five valid ways to color the current row:
- {Green Red Green}
- {Green Red Yellow}
- {Green Yellow Green}
- {Yellow Red Green}
- {Yellow Red Yellow}
- From the above observation, it is clear that three possibilities have ends with the same color, and two possibilities have ends with different colors.
- If the previous row is colored Red Green Yellow, the following four possibilities of coloring the current row exists:
- {Green Red Green}
- {Green Yellow Red}
- {Green Yellow Green}
- {Yellow Red Green}
- From the above observation, it is clear that possibilities have ends the same color, and two possibilities have ends with different colors.
- If the previous row is painted as Red Green Red, then there are the following five valid ways to color the current row:
- Therefore, based on the above observations, the following recurrence relation can be defined for the number of ways to paint the N rows:
Count of ways to color current row having ends of same color SN+1 = 3 * SN + 2DN
Count of ways to color current row having ends of different colors DN+1 = 2 * SN + 2DN
Total number of ways to paint all N rows is equal to the sum of SN and DN.
Below is the implementation of the above approach:
C++
// C++ program for the above approach#include <bits/stdc++.h>using namespace std;// Function to count the number// of ways to paint N * 3 grid// based on given conditionsvoid waysToPaint(int n){ // Count of ways to pain a // row with same colored ends int same = 6; // Count of ways to pain a row // with different colored ends int diff = 6; // Traverse up to (N - 1)th row for (int i = 0; i < n - 1; i++) { // Calculate the count of ways // to paint the current row // For same colored ends long sameTmp = 3 * same + 2 * diff; // For different colored ends long diffTmp = 2 * same + 2 * diff; same = sameTmp; diff = diffTmp; } // Print the total number of ways cout << (same + diff);}// Driver Codeint main(){ int N = 2; waysToPaint(N);}// This code is contributed by ukasp. |
Java
// Java program for the above approachimport java.io.*;import java.lang.*;import java.util.*;class GFG { // Function to count the number // of ways to paint N * 3 grid // based on given conditions static void waysToPaint(int n) { // Count of ways to pain a // row with same colored ends long same = 6; // Count of ways to pain a row // with different colored ends long diff = 6; // Traverse up to (N - 1)th row for (int i = 0; i < n - 1; i++) { // Calculate the count of ways // to paint the current row // For same colored ends long sameTmp = 3 * same + 2 * diff; // For different colored ends long diffTmp = 2 * same + 2 * diff; same = sameTmp; diff = diffTmp; } // Print the total number of ways System.out.println(same + diff); } // Driver code public static void main(String[] args) { int N = 2; // Function call waysToPaint(N); }} |
Python3
# Python3 program for the above approach# Function to count the number# of ways to paint N * 3 grid# based on given conditionsdef waysToPaint(n): # Count of ways to pain a # row with same colored ends same = 6 # Count of ways to pain a row # with different colored ends diff = 6 # Traverse up to (N - 1)th row for _ in range(n - 1): # Calculate the count of ways # to paint the current row # For same colored ends sameTmp = 3 * same + 2 * diff # For different colored ends diffTmp = 2 * same + 2 * diff same = sameTmp diff = diffTmp # Print the total number of ways print(same + diff)# Driver CodeN = 2waysToPaint(N) |
C#
// C# program for the above approachusing System;class GFG { // Function to count the number // of ways to paint N * 3 grid // based on given conditions static void waysToPaint(int n) { // Count of ways to pain a // row with same colored ends long same = 6; // Count of ways to pain a row // with different colored ends long diff = 6; // Traverse up to (N - 1)th row for (int i = 0; i < n - 1; i++) { // Calculate the count of ways // to paint the current row // For same colored ends long sameTmp = 3 * same + 2 * diff; // For different colored ends long diffTmp = 2 * same + 2 * diff; same = sameTmp; diff = diffTmp; } // Print the total number of ways Console.WriteLine(same + diff); } // Driver code static public void Main() { int N = 2; waysToPaint(N); }}// This code is contributed by offbeat |
Javascript
<script>// Javascript program for the above approach// Function to count the number// of ways to paint N * 3 grid// based on given conditionsfunction waysToPaint(n){ // Count of ways to pain a // row with same colored ends var same = 6; // Count of ways to pain a row // with different colored ends var diff = 6; // Traverse up to (N - 1)th row for(var i = 0; i < n - 1; i++) { // Calculate the count of ways // to paint the current row // For same colored ends var sameTmp = 3 * same + 2 * diff; // For different colored ends var diffTmp = 2 * same + 2 * diff; same = sameTmp; diff = diffTmp; } // Print the total number of ways document.write(same + diff);}// Driver codevar N = 2;// Function callwaysToPaint(N); // This code is contributed by Khushboogoyal499</script> |
Output:
12
Time Complexity: O(N)
Auxiliary Space: O(1)
Feeling lost in the world of random DSA topics, wasting time without progress? It’s time for a change! Join our DSA course, where we’ll guide you on an exciting journey to master DSA efficiently and on schedule.
Ready to dive in? Explore our Free Demo Content and join our DSA course, trusted by over 100,000 neveropen!
Ready to dive in? Explore our Free Demo Content and join our DSA course, trusted by over 100,000 neveropen!
