This article was published as a part of the Data Science Blogathon
Introduction
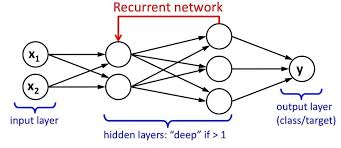
We have an input layer, a hidden layer, and an output layer. The input layer takes the input, activations functions are applied to the hidden layer, and finally, we receive the output.
In a deep neural network where multiple hidden layers are present. Each hidden layer is known by its weights and biases.
The weights and biases of these hidden layers are different. Hence each of these layers behaves differently/independently and so that we can’t combine them together. We should have the same weights and biases for these hidden layers to bind these hidden layers together.
Now we can combine these layers together because the weights and bias of all the hidden layers are the same now. All these hidden layers can be bound together in one single recurrent layer.
There are three types of Deep Neural Networks:
1. Artificial Neural Network
2. Convolutional Neural Network
3. Recurrent Neural Network
In this article, we will be focusing on Recurrent Neural Networks.
What are RNNs?
– A series of feed-forward neural networks in which the hidden nodes are connected in series.
– RNN has multiple series predictions, unlike CNN.
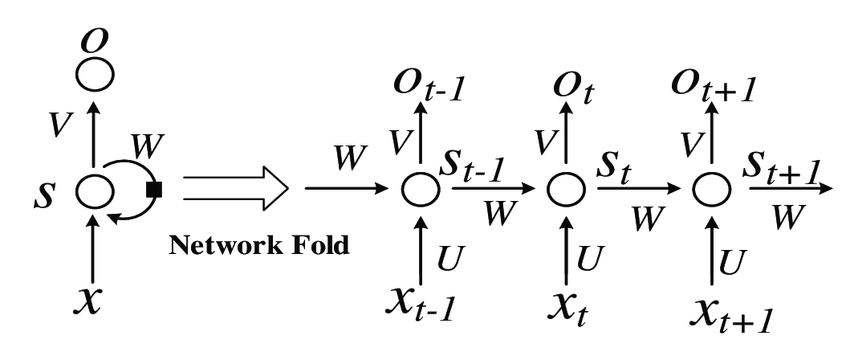
Image source: https://www.researchgate.net/publication/329330308/figure/fig1/AS:698826503495682@1543624630550/Basic-recurrent-neural-network-RNN-structure.png
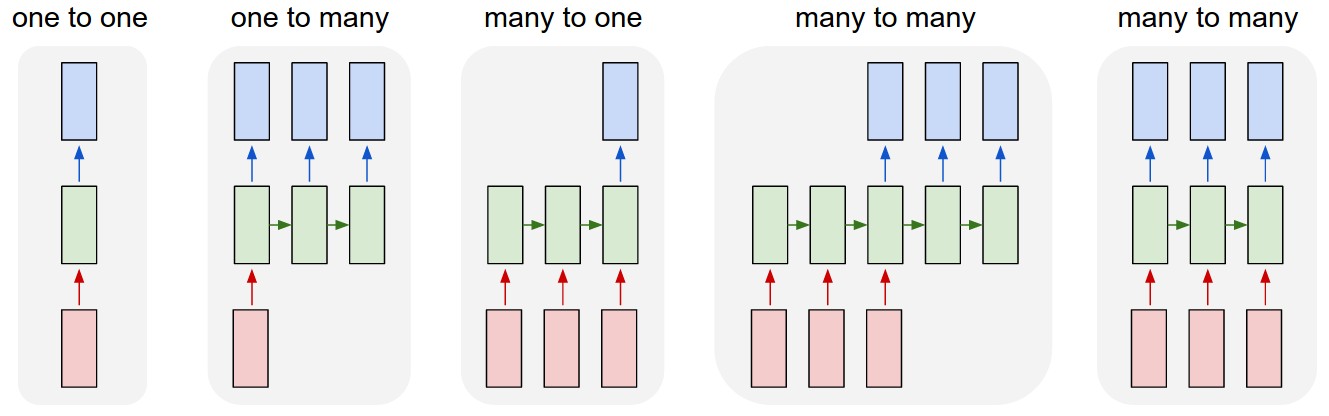
Types of RNNs
1. One to One: This is also called Vanilla Neural Network. It is used in such machine learning problems where it has a single input and single output
2. One to Many: It has a single input and multiple outputs. An example is Music Generation
3. Many to One: RNN takes a sequence of inputs and produces a single output. The examples are Sentiment classification, prediction of the next word.
4. Many to Many: RNN takes a sequence of inputs and produces a sequence of outputs. For example, Language Translation.
Improvements to RNN
– RNNs have a problem called vanishing gradient descent
– Hence there are two improvements over it
1.Gated Recurrent Unit (GRU)
2.Long Short Term Memory (LSTM))
– Among these more popular is LSTM more often used in time series
forecasting also.
Vanishing Gradient Problem
Before we build our first RNN, we need to understand the vanishing gradient problem. Let’s take a quick look at Vanishing Gradient Problem.
What is the Vanishing Gradient Problem?
The Vanishing Gradient Problem was discovered by Sepp Hochreiter, who is a German computer scientist who also had a role in the development of Recurrent Neural Networks in deep learning.
As its name says, the vanishing gradient problem is related to deep learning gradient descent algorithms. The gradient descent algorithm is then combined with a backpropagation algorithm to update the weights throughout the Neural Network. Recurrent neural network behaves a little differently due to the hidden layer of one observation is used to train the hidden layer of the next observation.
This vanishing gradient problem occurs when the backpropagation algorithm moves back through all the neurons of the neural network to update their weights.
Initialization of weights is one of the techniques that can be used to solve the Vanishing Gradient Problem. That is creating an initial value for weights in a neural network to prevent the backpropagation algorithm from assigning weights that are small.
Applications(Some of) of RNN
– Speech Recognition: Anyone speaking with a particular language, gets translated into different languages. And also voice is recognized by the machine.
– Language Translation: Using RNN, Text mining and Sentiment analysis can be carried out for Natural Language Processing (NLP).
– Image Recognition and its characterization: RNNs are used to capture an image by analyzing the present activities.
– Time Series Forecasting: Any time series forecasting problem, such as predicting the prices of stocks in a particular month/year, can be solved using an RNN.
Implementation Of RNN
Let us look at how to implement Time Series Forecasting using LSTM(Long Short Term Memory).
Now we will import some basic libraries to perform data frame functions.
Here I have used a dataset of Google Stock Price. You can download the dataset using this link. So there are two files in the given dataset as google_stock_price_train.csv and google_stock_price_test.csv. So first here we are going to take the training file.
Next, we have to perform normalization of data using scaling. Our data will be scaled into a specific format. So we need the MinMaxScaler library as well.
from sklearn.preprocessing import MinMaxScaler sc = MinMaxScaler(feature_range = (0, 1)) training_set_scaled = sc.fit_transform(training_set)
Now, we create a data structure with 60 timesteps and one output as an Array of x_train and y_train.
X_train = []
y_train = []
for i in range(60, 1258):
X_train.append(training_set_scaled[i-60:i, 0])
y_train.append(training_set_scaled[i, 0])
X_train, y_train = np.array(X_train), np.array(y_train)
Here we have done reshaping of x_train data.
X_train = np.reshape(X_train, (X_train.shape[0], X_train.shape[1], 1))
Now, the following libraries are required for building the RNN model and perform its operations. We have imported the Keras library and its packages.
from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM from keras.layers import Dropout
Let’s initialize our RNN.
regressor = Sequential()
Now, add the first layer of LSTM and some Dropout regularisation
regressor.add(LSTM(units = 50, return_sequences = True, input_shape = (X_train.shape[1], 1))) regressor.add(Dropout(0.2))
Now, add the second layer of LSTM and some Dropout regularisation
regressor.add(LSTM(units = 50, return_sequences = True)) regressor.add(Dropout(0.2))
Now, add the third layer of LSTM and some Dropout regularisation
regressor.add(LSTM(units = 50, return_sequences = True)) regressor.add(Dropout(0.2))
Now, add the fourth layer of LSTM and some Dropout regularisation
regressor.add(LSTM(units = 50)) regressor.add(Dropout(0.2))
Let’s add an output layer.
regressor.add(Dense(units = 1))
Next, we will compile our RNN model here.
regressor.compile(optimizer = 'adam', loss = 'mean_squared_error')
We are using a training dataset to fit the RNN model.
regressor.fit(X_train, y_train, epochs = 100, batch_size = 32)
Epoch 1/100 38/38 [==============================] - 4s 100ms/step - loss: 0.0419 0s - loss: Epoch 2/100 38/38 [==============================] - 4s 104ms/step - loss: 0.0058 Epoch 3/100 38/38 [==============================] - 4s 99ms/step - loss: 0.0060 Epoch 4/100 38/38 [==============================] - 4s 98ms/step - loss: 0.0051 Epoch 5/100 38/38 [==============================] - 4s 100ms/step - loss: 0.0050 Epoch 6/100 38/38 [==============================] - 4s 99ms/step - loss: 0.0045 Epoch 7/100 38/38 [==============================] - 4s 101ms/step - loss: 0.0047 Epoch 8/100 38/38 [==============================] - 4s 100ms/step - loss: 0.0046 Epoch 9/100 38/38 [==============================] - 4s 101ms/step - loss: 0.0044 Epoch 10/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0046 Epoch 11/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0043 Epoch 12/100 38/38 [==============================] - 4s 101ms/step - loss: 0.0041 Epoch 13/100 38/38 [==============================] - 4s 100ms/step - loss: 0.0047 Epoch 14/100 38/38 [==============================] - 4s 100ms/step - loss: 0.0035 Epoch 15/100 38/38 [==============================] - 4s 100ms/step - loss: 0.0039 Epoch 16/100 38/38 [==============================] - 4s 100ms/step - loss: 0.0038 Epoch 17/100 38/38 [==============================] - 4s 100ms/step - loss: 0.0035 Epoch 18/100 38/38 [==============================] - 4s 100ms/step - loss: 0.0035 Epoch 19/100 38/38 [==============================] - 4s 100ms/step - loss: 0.0034 Epoch 20/100 38/38 [==============================] - 4s 100ms/step - loss: 0.0036 Epoch 21/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0038 Epoch 22/100 38/38 [==============================] - 4s 100ms/step - loss: 0.0034 Epoch 23/100 38/38 [==============================] - 4s 101ms/step - loss: 0.0033 Epoch 24/100 38/38 [==============================] - 4s 101ms/step - loss: 0.0036 Epoch 25/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0035 Epoch 26/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0036 Epoch 27/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0031 Epoch 28/100 38/38 [==============================] - 4s 106ms/step - loss: 0.0032 Epoch 29/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0030 Epoch 30/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0030 Epoch 31/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0031 Epoch 32/100 38/38 [==============================] - 4s 101ms/step - loss: 0.0030 0s - lo Epoch 33/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0028 Epoch 34/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0030 Epoch 35/100 38/38 [==============================] - 4s 101ms/step - loss: 0.0025 Epoch 36/100 38/38 [==============================] - 4s 101ms/step - loss: 0.0028 Epoch 37/100 38/38 [==============================] - 4s 101ms/step - loss: 0.0032 Epoch 38/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0028 Epoch 39/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0031 Epoch 40/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0026 Epoch 41/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0026 Epoch 42/100 38/38 [==============================] - 4s 106ms/step - loss: 0.0027 Epoch 43/100 38/38 [==============================] - 4s 105ms/step - loss: 0.0027 Epoch 44/100 38/38 [==============================] - 4s 104ms/step - loss: 0.0023 Epoch 45/100 38/38 [==============================] - 4s 106ms/step - loss: 0.0023 Epoch 46/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0024 Epoch 47/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0024 0s - loss: 0.002 Epoch 48/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0025 Epoch 49/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0025 0s - lo Epoch 50/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0023 Epoch 51/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0023 Epoch 52/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0024 Epoch 53/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0022 Epoch 54/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0023 Epoch 55/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0022 Epoch 56/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0025 0s - loss Epoch 57/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0023 Epoch 58/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0022 Epoch 59/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0022 Epoch 60/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0021 Epoch 61/100 38/38 [==============================] - 4s 109ms/step - loss: 0.0021 Epoch 62/100 38/38 [==============================] - 4s 105ms/step - loss: 0.0020 Epoch 63/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0020 Epoch 64/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0022 0s - loss: 0.0 - ETA: 0s - loss: 0.002 Epoch 65/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0024 Epoch 66/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0021 Epoch 67/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0020 Epoch 68/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0019 Epoch 69/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0020 Epoch 70/100 38/38 [==============================] - 4s 106ms/step - loss: 0.0022 Epoch 71/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0020 Epoch 72/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0018 Epoch 73/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0020 Epoch 74/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0016 Epoch 75/100 38/38 [==============================] - 4s 104ms/step - loss: 0.0018 Epoch 76/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0018 Epoch 77/100 38/38 [==============================] - 4s 106ms/step - loss: 0.0019 Epoch 78/100 38/38 [==============================] - 4s 105ms/step - loss: 0.0017 Epoch 79/100 38/38 [==============================] - 4s 104ms/step - loss: 0.0019 Epoch 80/100 38/38 [==============================] - 4s 111ms/step - loss: 0.0018 Epoch 81/100 38/38 [==============================] - 5s 123ms/step - loss: 0.0017 Epoch 82/100 38/38 [==============================] - 4s 104ms/step - loss: 0.0017 Epoch 83/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0017 Epoch 84/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0015 Epoch 85/100 38/38 [==============================] - 4s 104ms/step - loss: 0.0015 Epoch 86/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0015 0s - los Epoch 87/100 38/38 [==============================] - 4s 101ms/step - loss: 0.0018 Epoch 88/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0015 Epoch 89/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0015 1s Epoch 90/100 38/38 [==============================] - 4s 101ms/step - loss: 0.0017 Epoch 91/100 38/38 [==============================] - 4s 101ms/step - loss: 0.0017 Epoch 92/100 38/38 [==============================] - 4s 101ms/step - loss: 0.0017 Epoch 93/100 38/38 [==============================] - 4s 103ms/step - loss: 0.0014 Epoch 94/100 38/38 [==============================] - 4s 104ms/step - loss: 0.0017 Epoch 95/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0016 Epoch 96/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0013 Epoch 97/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0014 Epoch 98/100 38/38 [==============================] - 4s 101ms/step - loss: 0.0015 Epoch 99/100 38/38 [==============================] - 4s 102ms/step - loss: 0.0014 Epoch 100/100 38/38 [==============================] - 4s 101ms/step - loss: 0.0014
Now our next part is to predict stock prices and visualize their results. Here we have used the real stock price of 2017 with data of google_stock_price.csv.
dataset_test = pd.read_csv('Google_Stock_Price_Test.csv')
real_stock_price = dataset_test.iloc[:, 1:2].values
Getting the predicted stock price of 2017
dataset_total = pd.concat((dataset_train['Open'], dataset_test['Open']), axis = 0)
inputs = dataset_total[len(dataset_total) - len(dataset_test) - 60:].values
inputs = inputs.reshape(-1,1)
inputs = sc.transform(inputs)
X_test = []
for i in range(60, 80):
X_test.append(inputs[i-60:i, 0])
X_test = np.array(X_test)
X_test = np.reshape(X_test, (X_test.shape[0], X_test.shape[1], 1))
predicted_stock_price = regressor.predict(X_test)
predicted_stock_price = sc.inverse_transform(predicted_stock_price)
The final step is to visualize our data results using the matplotlib library.
plt.plot(real_stock_price, color = 'red', label = 'Real Google Stock Price')
plt.plot(predicted_stock_price, color = 'blue', label = 'Predicted Google Stock Price')
plt.title('Google Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('Google Stock Price')
plt.legend()
plt.show()
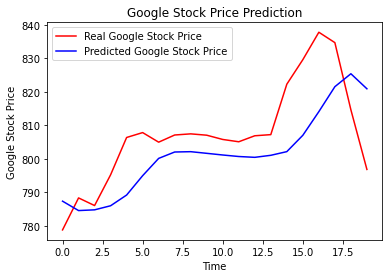
Shown image is a graph plotted by the above code.
Conclusion
Finally… We have successfully built our Basic Time Series Analysis model using Recurrent Neural Network. I hope you liked my article. Do share with your friends and colleagues. Thank You!
The media shown in this article are not owned by Analytics Vidhya and are used at the Author’s discretion.