This article was published as a part of the Data Science Blogathon
BERT is too kind — so this article will be touching on BERT and sequence relationships!
Abstract
A significant portion of NLP relies on the connection in highly-dimensional spaces. Typically an NLP processing will take any text, prepare it to generate a tremendous vector/array rendering said text — then make certain transformations.
It’s a highly-dimensional charm. At an exceptional level, there’s not much extra to it. We require to understand what is following in detail and execute this in Python too! So, let’s get incited.

Introduction
Sentence similarity is one of the most explicit examples of how compelling a highly-dimensional spell can be.
The thesis is this:
- Take a line of sentence, transform it into a vector.
- Take various other penalties, and change them into vectors.
- Spot sentences with the shortest distance (Euclidean) or tiniest angle (cosine similarity) among them.
- We instantly get a standard of semantic similarity connecting sentences.
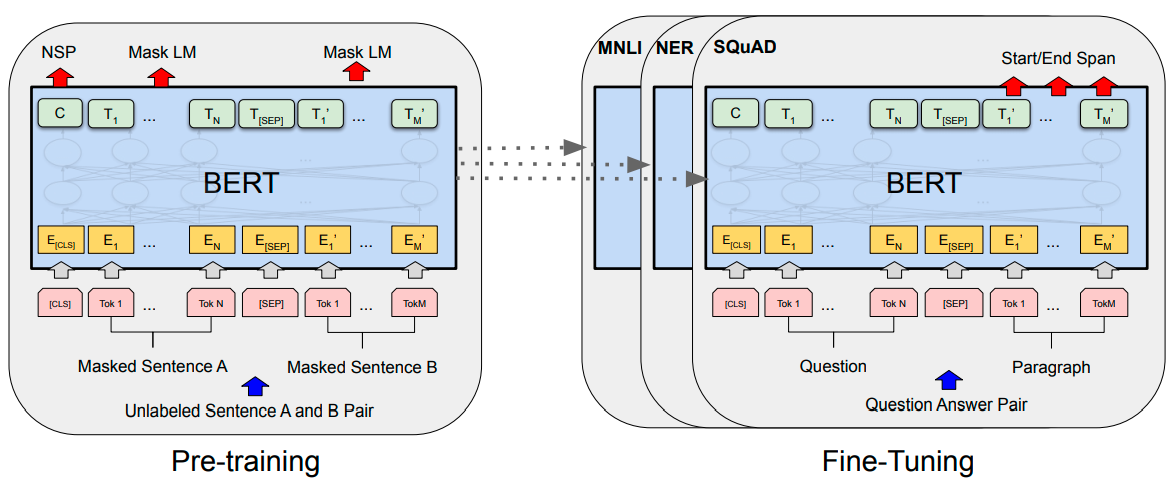
How BERT Helps?
BERT, as we previously stated — is a special MVP of NLP. And a massive part of this is underneath BERTs capability to embed the essence of words inside densely bound vectors.
We call them dense vectors because each value inside the vector has a value and has a purpose for holding that value — this is in contradiction to sparse vectors. Hence, as one-hot encoded vectors where the preponderance of proceedings is 0.
BERT is skilled at generating those dense vectors, and all encoder layer (there are numerous) outputs a collection of dense vectors.
For the BERT support, this will be a vector comprising 768 digits. Those 768 values have our mathematical representation of a particular token — which we can practice as contextual message embeddings.
Unit vector denoting each token (product by each encoder) is indeed watching tensor (768 by the number of tickets).
We can use these tensors and convert them to generate semantic designs of the input sequence. We can next take our similarity metrics and measure the corresponding similarity linking separate lines.
The easiest and most regularly extracted tensor is the last_hidden_state tensor, conveniently yield by the BERT model.
Of course, this is a moderately large tensor — at 512×768 — and we need a vector to implement our similarity measures.
To do this, we require to turn our last_hidden_states tensor to a vector of 768 tensors.
Building The Vector
For us to transform our last_hidden_states tensor into our desired vector — we use a mean pooling method.
Each of these 512 tokens has separate 768 values. This pooling work will take the average of all token embeddings and consolidate them into a unique 768 vector space, producing a ‘sentence vector’.
At the very time, we can’t just exercise the mean activation as is. We lack to estimate null padding tokens (which we should not hold).
Implementation
That’s noted on the theory and logic following the process, but how do we employ this in certainty?
We’ll describe two approaches — the comfortable way and the slightly more complicated way.
Method1: Sentence-Transformers
The usual straightforward approach for us to perform everything we just included is within the sentence; transformers library, which covers most of this rule into a few lines of code.
- First, we install sentence-transformers utilizing pip install sentence-transformers. This library uses HuggingFace’s transformers behind the pictures — so we can genuinely find sentence-transformers models here.
- We’ll be getting used to the best-base-no-mean-tokens model, which executes the very logic we’ve reviewed so far.
- (It also utilizes 128 input tokens, willingly than 512).
Let’s generate some sentences, initialize our representation, and encode the lines of words:
#Write some lines to encode (sentences 0 and 2 are both ideltical):
sen = [
"Three years later, the coffin was still full of Jello.",
"The fish dreamed of escaping the fishbowl and into the toilet where he saw his friend go.",
"The person box was packed with jelly many dozens of months later.",
"He found a leprechaun in his walnut shell."
]
from sentence_transformers import SentenceTransformer
model = SentenceTransformer('bert-base-nli-mean-tokens')
#Encoding:
sen_embeddings = model.encode(sen)
sen_embeddings.shape
Output: (4, 768)
Great, we now own four-sentence embeddings, each holding 768 values.
Now, something we do is use those embeddings and discover the cosine similarity linking each. So for line 0:
Three years later, the coffin was still full of Jello.
We can locate the most comparable sentence applying:
from sklearn.metrics.pairwise import cosine_similarity
#let's calculate cosine similarity for sentence 0:
cosine_similarity(
[sentence_embeddings[0]],
sentence_embeddings[1:]
)
Output: array([[0.33088914, 0.7219258 , 0.5548363 ]], dtype=float32)
Index Sentence Similarity 1 “The fish dreamed of escaping the fishbowl and into the toilet where he saw his friend go.” 0.3309 2 “The person box was packed with jelly many dozens of months later.” 0.7219 3 “He found a leprechaun in his walnut shell.” 0.5547
Now, here is the extra convenient and more intellectual approach.
Method2: Transformers And PyTorch
Before arriving at the second strategy, it is worth seeing that it does the identical thing as the above, but at one level more below.
- We want to achieve our transformation to the last_hidden_state to produce the sentence embedding with this plan. For this, we work the mean pooling operation.
- Additionally, before the mean pooling operation, we need to design last_hidden_state; here is the code for it:
from transformers import AutoTokenizer, AutoModel
import torch
#nitialize our model and tokenizer:
tokenizer = AutoTokenizer.from_pretrained('sentence-transformers/bert-base-nli-mean-tokens')
model = AutoModel.from_pretrained('sentence-transformers/bert-base-nli-mean-tokens')
###Tokenize the sentences like before:
sent = [
"Three years later, the coffin was still full of Jello.",
"The fish dreamed of escaping the fishbowl and into the toilet where he saw his friend go.",
"The person box was packed with jelly many dozens of months later.",
"He found a leprechaun in his walnut shell."
]
# initialize dictionary: stores tokenized sentences
token = {'input_ids': [], 'attention_mask': []}
for sentence in sent:
# encode each sentence, append to dictionary
new_token = tokenizer.encode_plus(sentence, max_length=128,
truncation=True, padding='max_length',
return_tensors='pt')
token['input_ids'].append(new_token['input_ids'][0])
token['attention_mask'].append(new_token['attention_mask'][0])
# reformat list of tensors to single tensor
token['input_ids'] = torch.stack(token['input_ids'])
token['attention_mask'] = torch.stack(token['attention_mask'])
#Process tokens through model: output = model(**token) output.keys()
Output: odict_keys([‘last_hidden_state’, ‘pooler_output’])
#The dense vector representations of text are contained within the outputs 'last_hidden_state' tensor embeddings = outputs.last_hidden_state embeddings
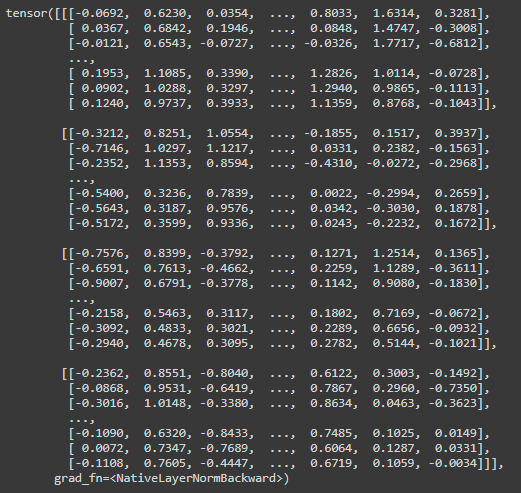
embeddings.shape
Output: torch.Size([4, 128, 768])
After writing our dense vector embeddings, we want to produce a mean pooling operation to form a single vector encoding, i.e., sentence embedding).
To achieve this mean pooling operation, we will require multiplying all values in our embeddings tensor by its corresponding attention_mask value to neglect non-real tokens.
# To perform this operation, we first resize our attention_mask tensor:
att_mask = tokens['attention_mask']
att_mask.shape
output: torch.Size([4, 128])
mask = att_mask.unsqueeze(-1).expand(embeddings.size()).float() mask.shape
Output: torch.Size([4, 128, 768])
mask_embeddings = embeddings * mask mask_embeddings.shape
Output: torch.Size([4, 128, 768])
#Then we sum the remained of the embeddings along axis 1: summed = torch.sum(mask_embeddings, 1) summed.shape
Output: torch.Size([4, 768])
#Then sum the number of values that must be given attention in each position of the tensor: summed_mask = torch.clamp(mask.sum(1), min=1e-9) summed_mask.shape
Output: torch.Size([4, 768])
mean_pooled = summed / summed_mask mean_pooled

Once we possess our dense vectors, we can compute the cosine similarity among each — which is the likewise logic we used previously:
from sklearn.metrics.pairwise import cosine_similarity
#Let's calculate cosine similarity for sentence 0:
# convert from PyTorch tensor to numpy array
mean_pooled = mean_pooled.detach().numpy()
# calculate
cosine_similarity(
[mean_pooled[0]],
mean_pooled[1:]
)
Output: array([[0.3308891 , 0.721926 , 0.55483633]], dtype=float32)
Index Sentence Similarity 1 “The fish dreamed of escaping the fishbowl and into the toilet where he saw his friend go.” 0.3309 2 “The person box was packed with jelly many dozens of months later.” 0.7219 3 “He found a leprechaun in his walnut shell.” 0.5548
We return around the identical results — the only distinction being that the cosine similarity for index three has slipped from 0.5547 to 0.5548 — an insignificant variation due to rounding.
End Notes
That’s all for this introduction to mapping the semantic similarity of sentences using BERT reviewing sentence-transformers and a lower-level explanation with Python-PyTorch and transformers.
I hope you’ve relished the article. Let me know if you hold any questions or suggestions via LinkedIn or in the remarks below.
Thanks for reading!
The media shown in this article are not owned by Analytics Vidhya and are used at the Author’s discretion.




