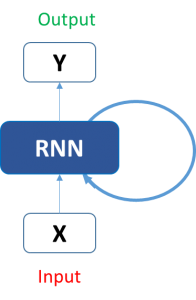
Introduction
Humans do not reboot their understanding of language each time we hear a sentence. Given an article, we grasp the context based on our previous understanding of those words. One of the defining characteristics we possess is our memory (or retention power).
Can an algorithm replicate this? The first technique that comes to mind is a neural network (NN). But the traditional NNs unfortunately cannot do this. Take an example of wanting to predict what comes next in a video. A traditional neural network will struggle to generate accurate results.
That’s where the concept of recurrent neural networks (RNNs) comes into play. RNNs have become extremely popular in the deep learning space which makes learning them even more imperative. A few real-world applications of RNN include:
- Speech recognition
- Machine translation
- Music composition
- Handwriting recognition
- Grammar learning
We can always leverage high-level Python libraries to code a RNN. So why code it from scratch? I firmly believe the best way to learn and truly ingrain a concept is to learn it from the ground up. And that’s what I’ll showcase in this tutorial.
This article assumes a basic understanding of recurrent neural networks. In case you need a quick refresher or are looking to learn the basics of RNN, I recommend going through the below articles first:
Table of Contents
- Flashback: A Recap of Recurrent Neural Network Concepts
- Sequence Prediction using RNN
- Building an RNN Model using Python
Flashback: A Recap of Recurrent Neural Network Concepts
Let’s quickly recap the core concepts behind recurrent neural networks.
We’ll do this using an example of sequence data, say the stocks of a particular firm. A simple machine learning model, or an Artificial Neural Network, may learn to predict the stock price based on a number of features, such as the volume of the stock, the opening value, etc. Apart from these, the price also depends on how the stock fared in the previous fays and weeks. For a trader, this historical data is actually a major deciding factor for making predictions.
In conventional feed-forward neural networks, all test cases are considered to be independent. Can you see how that’s a bad fit when predicting stock prices? The NN model would not consider the previous stock price values – not a great idea!
There is another concept we can lean on when faced with time sensitive data – Recurrent Neural Networks (RNN)!
A typical RNN looks like this:
This may seem intimidating at first. But once we unfold it, things start looking a lot simpler:
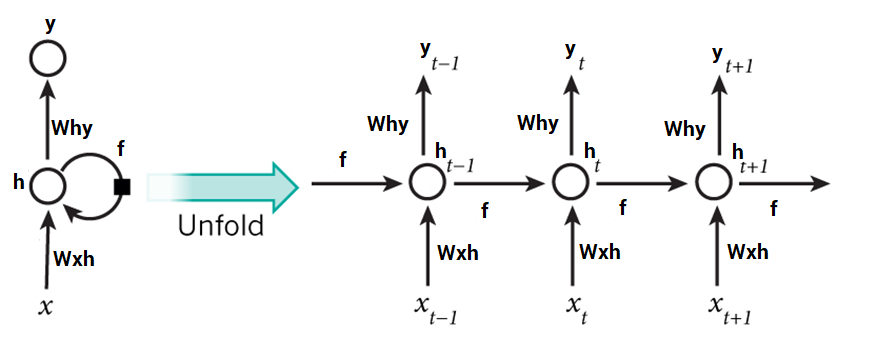
RNNs can solve our purpose of sequence handling to a great extent but not entirely.
Text is another good example of sequence data. Being able to predict what word or phrase comes after a given text could be a very useful asset. We want our models to write Shakespearean sonnets!
Now, RNNs are great when it comes to context that is short or small in nature. But in order to be able to build a story and remember it, our models should be able to understand the context behind the sequences, just like a human brain.
Sequence Prediction using RNN
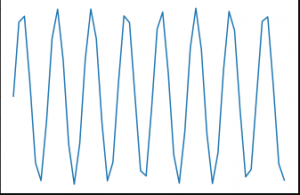
In this article, we will work on a sequence prediction problem using RNN. One of the simplest tasks for this is sine wave prediction. The sequence contains a visible trend and is easy to solve using heuristics. This is what a sine wave looks like:
We will first devise a recurrent neural network from scratch to solve this problem. Our RNN model should also be able to generalize well so we can apply it on other sequence problems.
We will formulate our problem like this – given a sequence of 50 numbers belonging to a sine wave, predict the 51st number in the series. Time to fire up your Jupyter notebook (or your IDE of choice)!
Coding RNN using Python
Step 0: Data Preparation
Ah, the inevitable first step in any data science project – preparing the data before we do anything else.
What does our network model expect the data to be like? It would accept a single sequence of length 50 as input. So the shape of the input data will be:
(number_of_records x length_of_sequence x types_of_sequences)
Here, types_of_sequences is 1, because we have only one type of sequence – the sine wave.
On the other hand, the output would have only one value for each record. This will of course be the 51st value in the input sequence. So it’s shape would be:
(number_of_records x types_of_sequences) #where types_of_sequences is 1
Let’s dive into the code. First, import the necessary libraries:
%pylab inline import math
To create a sine wave like data, we will use the sine function from Python’s math library:
sin_wave = np.array([math.sin(x) for x in np.arange(200)])
Visualizing the sine wave we’ve just generated:
plt.plot(sin_wave[:50])
Python Code:
X_val = [] Y_val = [] for i in range(num_records - 50, num_records): X_val.append(sin_wave[i:i+seq_len]) Y_val.append(sin_wave[i+seq_len]) X_val = np.array(X_val) X_val = np.expand_dims(X_val, axis=2) Y_val = np.array(Y_val) Y_val = np.expand_dims(Y_val, axis=1)
Step 1: Create the Architecture for our RNN model
Our next task is defining all the necessary variables and functions we’ll use in the RNN model. Our model will take in the input sequence, process it through a hidden layer of 100 units, and produce a single valued output:
learning_rate = 0.0001 nepoch = 25 T = 50 # length of sequence hidden_dim = 100 output_dim = 1 bptt_truncate = 5 min_clip_value = -10 max_clip_value = 10
We will then define the weights of the network:
U = np.random.uniform(0, 1, (hidden_dim, T)) W = np.random.uniform(0, 1, (hidden_dim, hidden_dim)) V = np.random.uniform(0, 1, (output_dim, hidden_dim))
Here,
- U is the weight matrix for weights between input and hidden layers
- V is the weight matrix for weights between hidden and output layers
- W is the weight matrix for shared weights in the RNN layer (hidden layer)
Finally, we will define the activation function, sigmoid, to be used in the hidden layer:
def sigmoid(x): return 1 / (1 + np.exp(-x))
Step 2: Train the Model
Now that we have defined our model, we can finally move on with training it on our sequence data. We can subdivide the training process into smaller steps, namely:
Step 2.1 : Check the loss on training data
Step 2.1.1 : Forward Pass
Step 2.1.2 : Calculate Error
Step 2.2 : Check the loss on validation data
Step 2.2.1 : Forward Pass
Step 2.2.2 : Calculate Error
Step 2.3 : Start actual training
Step 2.3.1 : Forward Pass
Step 2.3.2 : Backpropagate Error
Step 2.3.3 : Update weights
We need to repeat these steps until convergence. If the model starts to overfit, stop! Or simply pre-define the number of epochs.
Step 2.1: Check the loss on training data
We will do a forward pass through our RNN model and calculate the squared error for the predictions for all records in order to get the loss value.
for epoch in range(nepoch): # check loss on train loss = 0.0 # do a forward pass to get prediction for i in range(Y.shape[0]): x, y = X[i], Y[i] # get input, output values of each record prev_s = np.zeros((hidden_dim, 1)) # here, prev-s is the value of the previous activation of hidden layer; which is initialized as all zeroes for t in range(T): new_input = np.zeros(x.shape) # we then do a forward pass for every timestep in the sequence new_input[t] = x[t] # for this, we define a single input for that timestep mulu = np.dot(U, new_input) mulw = np.dot(W, prev_s) add = mulw + mulu s = sigmoid(add) mulv = np.dot(V, s) prev_s = s # calculate error loss_per_record = (y - mulv)**2 / 2 loss += loss_per_record loss = loss / float(y.shape[0])
Step 2.2: Check the loss on validation data
We will do the same thing for calculating the loss on validation data (in the same loop):
# check loss on val val_loss = 0.0 for i in range(Y_val.shape[0]): x, y = X_val[i], Y_val[i] prev_s = np.zeros((hidden_dim, 1)) for t in range(T): new_input = np.zeros(x.shape) new_input[t] = x[t] mulu = np.dot(U, new_input) mulw = np.dot(W, prev_s) add = mulw + mulu s = sigmoid(add) mulv = np.dot(V, s) prev_s = s loss_per_record = (y - mulv)**2 / 2 val_loss += loss_per_record val_loss = val_loss / float(y.shape[0]) print('Epoch: ', epoch + 1, ', Loss: ', loss, ', Val Loss: ', val_loss)
You should get the below output:
Epoch: 1 , Loss: [[101185.61756671]] , Val Loss: [[50591.0340148]] ... ...
Step 2.3: Start actual training
We will now start with the actual training of the network. In this, we will first do a forward pass to calculate the errors and a backward pass to calculate the gradients and update them. Let me show you these step-by-step so you can visualize how it works in your mind.
Step 2.3.1: Forward Pass
In the forward pass:
- We first multiply the input with the weights between input and hidden layers
- Add this with the multiplication of weights in the RNN layer. This is because we want to capture the knowledge of the previous timestep
- Pass it through a sigmoid activation function
- Multiply this with the weights between hidden and output layers
- At the output layer, we have a linear activation of the values so we do not explicitly pass the value through an activation layer
- Save the state at the current layer and also the state at the previous timestep in a dictionary
Here is the code for doing a forward pass (note that it is in continuation of the above loop):
# train model for i in range(Y.shape[0]): x, y = X[i], Y[i] layers = [] prev_s = np.zeros((hidden_dim, 1)) dU = np.zeros(U.shape) dV = np.zeros(V.shape) dW = np.zeros(W.shape) dU_t = np.zeros(U.shape) dV_t = np.zeros(V.shape) dW_t = np.zeros(W.shape) dU_i = np.zeros(U.shape) dW_i = np.zeros(W.shape) # forward pass for t in range(T): new_input = np.zeros(x.shape) new_input[t] = x[t] mulu = np.dot(U, new_input) mulw = np.dot(W, prev_s) add = mulw + mulu s = sigmoid(add) mulv = np.dot(V, s) layers.append({'s':s, 'prev_s':prev_s}) prev_s = s
Step 2.3.2 : Backpropagate Error
After the forward propagation step, we calculate the gradients at each layer, and backpropagate the errors. We will use truncated back propagation through time (TBPTT), instead of vanilla backprop. It may sound complex but its actually pretty straight forward.
The core difference in BPTT versus backprop is that the backpropagation step is done for all the time steps in the RNN layer. So if our sequence length is 50, we will backpropagate for all the timesteps previous to the current timestep.
If you have guessed correctly, BPTT seems very computationally expensive. So instead of backpropagating through all previous timestep , we backpropagate till x timesteps to save computational power. Consider this ideologically similar to stochastic gradient descent, where we include a batch of data points instead of all the data points.
Here is the code for backpropagating the errors:
# derivative of pred dmulv = (mulv - y) # backward pass for t in range(T): dV_t = np.dot(dmulv, np.transpose(layers[t]['s'])) dsv = np.dot(np.transpose(V), dmulv) ds = dsv dadd = add * (1 - add) * ds dmulw = dadd * np.ones_like(mulw) dprev_s = np.dot(np.transpose(W), dmulw) for i in range(t-1, max(-1, t-bptt_truncate-1), -1): ds = dsv + dprev_s dadd = add * (1 - add) * ds dmulw = dadd * np.ones_like(mulw) dmulu = dadd * np.ones_like(mulu) dW_i = np.dot(W, layers[t]['prev_s']) dprev_s = np.dot(np.transpose(W), dmulw) new_input = np.zeros(x.shape) new_input[t] = x[t] dU_i = np.dot(U, new_input) dx = np.dot(np.transpose(U), dmulu) dU_t += dU_i dW_t += dW_i dV += dV_t dU += dU_t dW += dW_t
Step 2.3.3 : Update weights
Lastly, we update the weights with the gradients of weights calculated. One thing we have to keep in mind that the gradients tend to explode if you don’t keep them in check.This is a fundamental issue in training neural networks, called the exploding gradient problem. So we have to clamp them in a range so that they dont explode. We can do it like this
if dU.max() > max_clip_value: dU[dU > max_clip_value] = max_clip_value if dV.max() > max_clip_value: dV[dV > max_clip_value] = max_clip_value if dW.max() > max_clip_value: dW[dW > max_clip_value] = max_clip_value if dU.min() < min_clip_value: dU[dU < min_clip_value] = min_clip_value if dV.min() < min_clip_value: dV[dV < min_clip_value] = min_clip_value if dW.min() < min_clip_value: dW[dW < min_clip_value] = min_clip_value # update U -= learning_rate * dU V -= learning_rate * dV W -= learning_rate * dW
On training the above model, we get this output:
Epoch: 1 , Loss: [[101185.61756671]] , Val Loss: [[50591.0340148]] Epoch: 2 , Loss: [[61205.46869629]] , Val Loss: [[30601.34535365]] Epoch: 3 , Loss: [[31225.3198258]] , Val Loss: [[15611.65669247]] Epoch: 4 , Loss: [[11245.17049551]] , Val Loss: [[5621.96780111]] Epoch: 5 , Loss: [[1264.5157739]] , Val Loss: [[632.02563908]] Epoch: 6 , Loss: [[20.15654115]] , Val Loss: [[10.05477285]] Epoch: 7 , Loss: [[17.13622839]] , Val Loss: [[8.55190426]] Epoch: 8 , Loss: [[17.38870495]] , Val Loss: [[8.68196484]] Epoch: 9 , Loss: [[17.181681]] , Val Loss: [[8.57837827]] Epoch: 10 , Loss: [[17.31275313]] , Val Loss: [[8.64199652]] Epoch: 11 , Loss: [[17.12960034]] , Val Loss: [[8.54768294]] Epoch: 12 , Loss: [[17.09020065]] , Val Loss: [[8.52993502]] Epoch: 13 , Loss: [[17.17370113]] , Val Loss: [[8.57517454]] Epoch: 14 , Loss: [[17.04906914]] , Val Loss: [[8.50658127]] Epoch: 15 , Loss: [[16.96420184]] , Val Loss: [[8.46794248]] Epoch: 16 , Loss: [[17.017519]] , Val Loss: [[8.49241316]] Epoch: 17 , Loss: [[16.94199493]] , Val Loss: [[8.45748739]] Epoch: 18 , Loss: [[16.99796892]] , Val Loss: [[8.48242177]] Epoch: 19 , Loss: [[17.24817035]] , Val Loss: [[8.6126231]] Epoch: 20 , Loss: [[17.00844599]] , Val Loss: [[8.48682234]] Epoch: 21 , Loss: [[17.03943262]] , Val Loss: [[8.50437328]] Epoch: 22 , Loss: [[17.01417255]] , Val Loss: [[8.49409597]] Epoch: 23 , Loss: [[17.20918888]] , Val Loss: [[8.5854792]] Epoch: 24 , Loss: [[16.92068017]] , Val Loss: [[8.44794633]] Epoch: 25 , Loss: [[16.76856238]] , Val Loss: [[8.37295808]]
Looking good! Time to get the predictions and plot them to get a visual sense of what we’ve designed.
Step 3: Get predictions
We will do a forward pass through the trained weights to get our predictions:
preds = [] for i in range(Y.shape[0]): x, y = X[i], Y[i] prev_s = np.zeros((hidden_dim, 1)) # Forward pass for t in range(T): mulu = np.dot(U, x) mulw = np.dot(W, prev_s) add = mulw + mulu s = sigmoid(add) mulv = np.dot(V, s) prev_s = s preds.append(mulv) preds = np.array(preds)
Plotting these predictions alongside the actual values:
plt.plot(preds[:, 0, 0], 'g') plt.plot(Y[:, 0], 'r') plt.show()
preds = [] for i in range(Y_val.shape[0]): x, y = X_val[i], Y_val[i] prev_s = np.zeros((hidden_dim, 1)) # For each time step... for t in range(T): mulu = np.dot(U, x) mulw = np.dot(W, prev_s) add = mulw + mulu s = sigmoid(add) mulv = np.dot(V, s) prev_s = s preds.append(mulv) preds = np.array(preds) plt.plot(preds[:, 0, 0], 'g') plt.plot(Y_val[:, 0], 'r') plt.show()
from sklearn.metrics import mean_squared_error math.sqrt(mean_squared_error(Y_val[:, 0] * max_val, preds[:, 0, 0] * max_val))
0.127191931509431
End Notes
I cannot stress enough how useful RNNs are when working with sequence data. I implore you all to take this learning and apply it on a dataset. Take a NLP problem and see if you can find a solution for it. You can always reach out to me in the comments section below if you have any questions.
In this article, we learned how to create a recurrent neural network model from scratch by using just the numpy library. You can of course use a high-level library like Keras or Caffe but it is essential to know the concept you’re implementing.
Do share your thoughts, questions and feedback regarding this article below. Happy learning!