Introduction
In a typical ‘from think to buy’ customer journey, a customer goes through multiple touch points before zeroing in on the final product to buy. This is even more prominent in the case of e-commerce sales. It is relatively easier to track which are the different touch points the customer has encountered before making the final purchase.

Source: MarTech Today
As marketing moves more and more towards the consumer driven side of things, identifying the right channels to target customers has become critical for companies. This helps companies optimise their marketing spend and target the right customers in the right places.
More often than not, companies usually invest in the last channel which customers encounter before making the final purchase. However, this may not always be the right approach. There are multiple channels preceding that channel which eventually drive the customer conversion. The underlying concept to study this behavior is known as ‘multi-channel attribution modeling.’
In this article, we look at what channel attribution is and how it ties into the concept of Markov chains. We’ll also take a case study of an e-commerce company to understand how this concept works, both theoretically and practically (using R).
Table of Contents
- What is Channel Attribution?
- Markov Chains
- Removal Effect
- Case Study of an E-Commerce Company
- Implementation in R
What is Channel Attribution?
Google Analytics offers a standard set of rules for attribution modeling. As per Google, “An attribution model is the rule, or set of rules, that determines how credit for sales and conversions is assigned to touchpoints in conversion paths. For example, the Last Interaction model in Analytics assigns 100% credit to the final touchpoints (i.e., clicks) that immediately precede sales or conversions. In contrast, the First Interaction model assigns 100% credit to touchpoints that initiate conversion paths.”
We will see the last interaction model and first interaction model later in this article. Before that, let’s take a small example and understand channel attribution a little further. Let’s say we have a transition diagram as shown below:
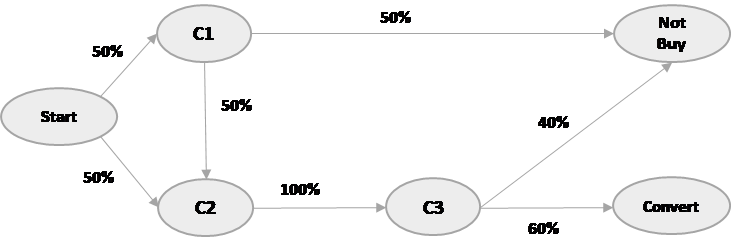
In the above scenario, a customer can either start their journey through channel ‘C1’ or channel ‘C2’. The probability of starting with either C1 or C2 is 50% (or 0.5) each. Let’s calculate the overall probability of conversion first and then go further to see the effect of each of the channels.
P(conversion) = P(C1 -> C2 -> C3 -> Conversion) + P(C2 -> C3 -> Conversion)
= 0.5*0.5*1*0.6 + 0.5*1*0.6
= 0.15 + 0.3
= 0.45
Markov Chains
Markov chains is a process which maps the movement and gives a probability distribution, for moving from one state to another state. A Markov Chain is defined by three properties:
- State space – set of all the states in which process could potentially exist
- Transition operator –the probability of moving from one state to other state
- Current state probability distribution – probability distribution of being in any one of the states at the start of the process
We know the stages through which we can pass, the probability of moving from each of the paths and we know the current state. This looks similar to Markov chains, doesn’t it?
Removal Effect
This is, in fact, an application of a Markov chains. We will come back to this later; let’s stick to our example for now. If we were to figure out what is the contribution of channel 1 in our customer’s journey from start to end conversion, we will use the principle of removal effect. Removal effect principle says that if we want to find the contribution of each channel in the customer journey, we can do so by removing each channel and see how many conversions are happening without that channel being in place.
For example, let’s assume we have to calculate the contribution of channel C1. We will remove the channel C1 from the model and see how many conversions are happening without C1 in the picture, viz-a-viz total conversion when all the channels are intact. Let’s calculate for channel C1:
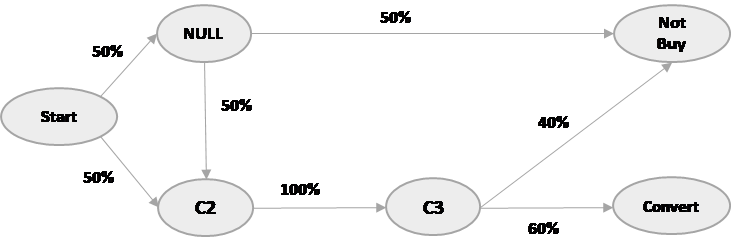
P(Conversion after removing C1) = P(C2 -> C3 -> Convert)
= 0.5*1*0.6
= 0.3
30% customer interactions can be converted without channel C1 being in place; while with C1 intact, 45% interactions can be converted. So, the removal effect of C1 is
0.3/0.45 = 0.666.
The removal effect of C2 and C3 is 1 (you may try calculating it, but think intuitively. If we were to remove either C2 or C3, will we be able to complete any conversion?).
This is a very useful application of Markov chains. In the above case, all the channels – C1, C2, C3 (at different stages) – are called transition states; while the probability of moving from one channel to another channel is called transition probability.
Customer journey, which is a sequence of channels, can be considered as a chain in a directed Markov graph where each vertex is a state (channel/touch-point), and each edge represents transition probability of moving from one state to another. Since the probability of reaching a state depends only on the previous state, it can be considered as a memory-less Markov chain.
Case Study of an E-Commerce Company
Let’s take a real-life case study and see how we can implement channel attribution modeling.
An e-commerce company conducted a survey and collected data from its customers. This can be considered as representative population. In the survey, the company collected data about the various touch points where customers visit before finally purchasing the product on its website.
In total, there are 19 channels where customers can encounter the product or the product advertisement. After the 19 channels, there are three more cases:
- #20 – customer has decided which device to buy;
- #21 – customer has made the final purchase, and;
- #22 – customer hasn’t decided yet.
The overall categories of channels are as below:
| Category | Channel |
| Website (1,2,3) | Company’s website or competitor’s website |
| Research Reports (4,5,6,7,8) | Industry Advisory Research Reports |
| Online/Reviews (9,10) | Organic Searches, Forums |
| Price Comparison (11) | Aggregators |
| Friends (12,13) | Social Network |
| Expert (14) | Expert online or offline |
| Retail Stores (15,16,17) | Physical Stores |
| Misc. (18,19) | Others such as Promotional Campaigns at various location |
Now, we need to help the e-commerce company in identifying the right strategy for investing in marketing channels. Which channels should be focused on? Which channels should the company invest in? We’ll figure this out using R in the following section.
Implementation using R
Let’s move ahead and try the implementation in R and check the results. You can download the dataset here and follow along as we go.
#Install the libraries
install.packages("ChannelAttribution")
install.packages("ggplot2")
install.packages("reshape")
install.packages("dplyr")
install.packages("plyr")
install.packages("reshape2")
install.packages("markovchain")
install.packages("plotly")
#Load the libraries
library("ChannelAttribution")
library("ggplot2")
library("reshape")
library("dplyr")
library("plyr")
library("reshape2")
library("markovchain")
library("plotly")
#Read the data into R
> channel = read.csv("Channel_attribution.csv", header = T)
> head(channel)
Output:
| R05A.01 | R05A.02 | R05A.03 | R05A.04 | ….. | R05A.18 | R05A.19 | R05A.20 |
| 16 | 4 | 3 | 5 | NA | NA | NA | |
| 2 | 1 | 9 | 10 | NA | NA | NA | |
| 9 | 13 | 20 | 16 | NA | NA | NA | |
| 8 | 15 | 20 | 21 | NA | NA | NA | |
| 16 | 9 | 13 | 20 | NA | NA | NA | |
| 1 | 11 | 8 | 4 | NA | NA | NA |
We will do some data processing to bring it to a stage where we can use it as an input in the model. Then, we will identify which customer journeys have gone to the final conversion (in our case, all the journeys have reached final conversion state).
We will create a variable ‘path’ in a specific format which can be fed as an input to the model. Also, we will find out the total occurrences of each path using the ‘dplyr’ package.
> for(row in 1:nrow(channel))
{
if(21 %in% channel[row,]){channel$convert[row] = 1}
}
> column = colnames(channel)
> channel$path = do.call(paste, c(channel[column], sep = " > "))
> head(channel$path)
[1] "16 > 4 > 3 > 5 > 10 > 8 > 6 > 8 > 13 > 20 > 21 > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > 1"
[2] "2 > 1 > 9 > 10 > 1 > 4 > 3 > 21 > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > 1"
[3] "9 > 13 > 20 > 16 > 15 > 21 > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > 1"
[4] "8 > 15 > 20 > 21 > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > 1"
[5] "16 > 9 > 13 > 20 > 21 > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > 1"
[6] "1 > 11 > 8 > 4 > 9 > 21 > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > NA > 1"
> for(row in 1:nrow(channel))
{
channel$path[row] = strsplit(channel$path[row], " > 21")[[1]][1]
}
> channel_fin = channel[,c(23,22)]
> channel_fin = ddply(channel_fin,~path,summarise, conversion= sum(convert))
> head(channel_fin)
Output:
| path | conversion |
| 1 > 1 > 1 > 20 | 1 |
| 1 > 1 > 12 > 12 | 1 |
| 1 > 1 > 14 > 13 > 12 > 20 | 1 |
| 1 > 1 > 3 > 13 > 3 > 20 | 1 |
| 1 > 1 > 3 > 17 > 17 | 1 |
| > 1 > 6 > 1 > 12 > 20 > 12 | 1 |
> Data = channel_fin > head(Data)
Output:
| path | conversion |
| 1 > 1 > 1 > 20 | 1 |
| 1 > 1 > 12 > 12 | 1 |
| 1 > 1 > 14 > 13 > 12 > 20 | 1 |
| 1 > 1 > 3 > 13 > 3 > 20 | 1 |
| 1 > 1 > 3 > 17 > 17 | 1 |
| 1 > 1 > 6 > 1 > 12 > 20 > 12 | 1 |
Now, we will create a heuristic model and a Markov model, combine the two, and then check the final results.
> H <- heuristic_models(Data, 'path', 'conversion', var_value='conversion') > H
Output:
| channel_name | first_touch_conversions | ….. | linear_touch_conversions | linear_touch_value |
| 1 | 130 | 73.773661 | 73.773661 | |
| 20 | 0 | 473.998171 | 473.998171 | |
| 12 | 75 | 76.127863 | 76.127863 | |
| 14 | 34 | 56.335744 | 56.335744 | |
| 13 | 320 | 204.039552 | 204.039552 | |
| 3 | 168 | 117.609677 | 117.609677 | |
| 17 | 31 | 76.583847 | 76.583847 | |
| 6 | 50 | 54.707124 | 54.707124 | |
| 8 | 56 | 53.677862 | 53.677862 | |
| 10 | 547 | 211.822393 | 211.822393 | |
| 11 | 66 | 107.109048 | 107.109048 | |
| 16 | 111 | 156.049086 | 156.049086 | |
| 2 | 199 | 94.111668 | 94.111668 | |
| 4 | 231 | 250.784033 | 250.784033 | |
| 7 | 26 | 33.435991 | 33.435991 | |
| 5 | 62 | 74.900402 | 74.900402 | |
| 9 | 250 | 194.07169 | 194.07169 | |
| 15 | 22 | 65.159225 | 65.159225 | |
| 18 | 4 | 5.026587 | 5.026587 | |
| 19 | 10 | 12.676375 | 12.676375 |
> M <- markov_model(Data, 'path', 'conversion', var_value='conversion', order = 1)> M
Output:
| channel_name | total_conversion | total_conversion_value |
| 1 | 82.482961 | 82.482961 |
| 20 | 432.40615 | 432.40615 |
| 12 | 83.942587 | 83.942587 |
| 14 | 63.08676 | 63.08676 |
| 13 | 195.751556 | 195.751556 |
| 3 | 122.973752 | 122.973752 |
| 17 | 83.866724 | 83.866724 |
| 6 | 63.280828 | 63.280828 |
| 8 | 61.016115 | 61.016115 |
| 10 | 209.035208 | 209.035208 |
| 11 | 118.563707 | 118.563707 |
| 16 | 158.692238 | 158.692238 |
| 2 | 98.067199 | 98.067199 |
| 4 | 223.709091 | 223.709091 |
| 7 | 41.919248 | 41.919248 |
| 5 | 81.865473 | 81.865473 |
| 9 | 179.483376 | 179.483376 |
| 15 | 70.360777 | 70.360777 |
| 18 | 5.950827 | 5.950827 |
| 19 | 15.545424 | 15.545424 |
Before going further, let’s first understand what a few of the terms we’ve seen above mean.
First Touch Conversion: The conversion happening through the channel when that channel is the first touch point for a customer. 100% credit is given to the first touch point.
Last Touch Conversion: The conversion happening through the channel when that channel is the last touch point for a customer. 100% credit is given to the last touch point.
Linear Touch Conversion: All channels/touch points are given equal credit in the conversion.
Getting back to the R code, let’s merge the two models and represent the output in a visually appealing manner which is easier to understand.
# Merges the two data frames on the "channel_name" column.
R <- merge(H, M, by='channel_name')
# Select only relevant columns
R1 <- R[, (colnames(R) %in %c('channel_name', 'first_touch_conversions', 'last_touch_conversions', 'linear_touch_conversions', 'total_conversion'))]
# Transforms the dataset into a data frame that ggplot2 can use to plot the outcomes
R1 <- melt(R1, id='channel_name')
# Plot the total conversions
ggplot(R1, aes(channel_name, value, fill = variable)) +
geom_bar(stat='identity', position='dodge') +
ggtitle('TOTAL CONVERSIONS') +
theme(axis.title.x = element_text(vjust = -2)) +
theme(axis.title.y = element_text(vjust = +2)) +
theme(title = element_text(size = 16)) +
theme(plot.title=element_text(size = 20)) +
ylab("")
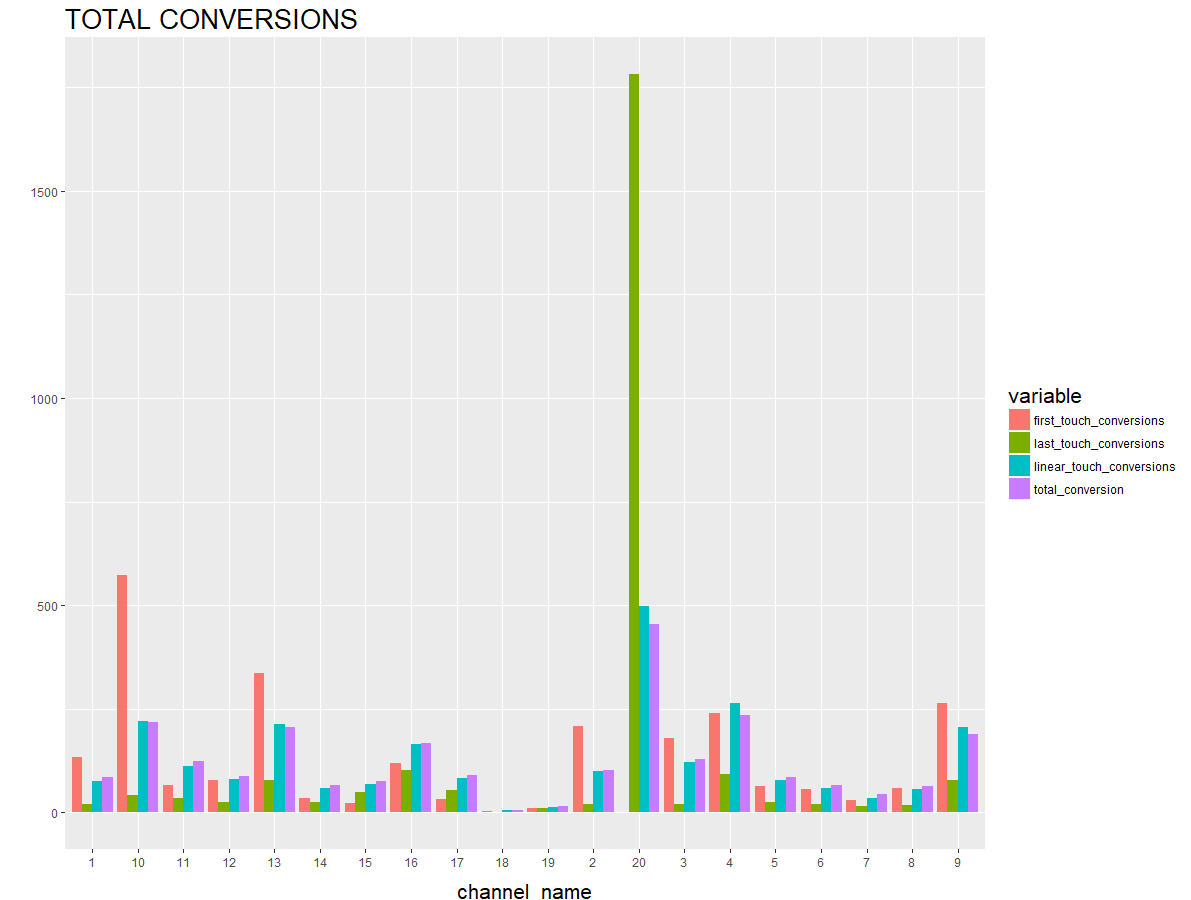
The scenario is clearly visible from the above graph. From the first touch conversion perspective, channel 10, channel 13, channel 2, channel 4 and channel 9 are quite important; while from the last touch perspective, channel 20 is the most important (in our case, it should be because the customer has decided which product to buy). In terms of linear touch conversion, channel 20, channel 4 and channel 9 are coming out to be important. From the total conversions perspective, channel 10, 13, 20, 4 and 9 are quite important.
End Notes
In the above chart we have been able to figure out which are the important channels for us to focus on and which can be discarded or ignored. This case gives us a very good insight into the application of Markov chain models in the customer analytics space. E-commerce companies can now confidently create their marketing strategy and distribute their marketing budget using data driven insights.
Author Bio:
This article was contributed by Perceptive Analytics. Chaitanya Sagar, Prudhvi Potuganti and Saneesh Veetil developed this article.
Perceptive Analytics provides data analytics, data visualization, business intelligence and reporting services to e-commerce, retail, healthcare and pharmaceutical industries. Our client roster includes Fortune 500 and NYSE listed companies in the USA and India.




