This article was published as a part of the Data Science Blogathon.

Source: totaljobs.com
Introduction
Transformers have become a powerful tool for different natural language processing tasks. The impressive performance of the transformer is mainly attributed to its self-attention mechanism. However, training big Transformers with long sequences is impossible in most cases due to their quadratic complexity. To workaround this limitation, Nystromformer was proposed.
In this article, I have compiled a list of six imperative questions on Nyströmformer that could help you become more familiar with the topic and help you succeed in your next interview!
Interview Questions on Nyströmformer
Question1: When compared to RNNs, which key element was responsible for impressive performance gain in transformers? Explain in detail.
Answer: The main element that made it possible for transformers to work excellently was self-attention. It computes a weighted average of feature representations with the weight proportional to a similarity score between pairs of representations.
In essence, self-attention encodes other tokens’ impact/influence/dependence on each specific token of a given input sequence.

Figure 1: Attention Mechanism (Source: Kaggle)
Formally, an input sequence (X) of n tokens is linearly projected using three matrices WQ,
WK, and WV to extract feature representations Q (query), K (key), and V (value), with the dimension of query equal to the dimension of key dk = dq. The outputs Q, K, and V are computed as follows:
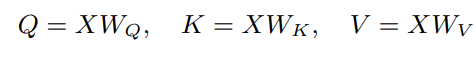
So, self-attention is defined as:
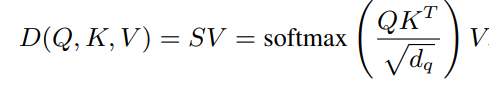
where softmax is a row-wise softmax normalization function; hence, each element in the softmax matrix S is dependent on all other elements in the same row.
Question 2: What are the drawbacks imposed by self-attention?
Answer: Yes. Despite being beneficial, self-attention is an efficiency bottleneck because it has a memory and time complexity of O(n2 ), where n is the length of an input sequence. This results in high memory and computational requirements for training large Transformer-based models, which has limited its application to longer sequences.
For example, with a single V100, training a BERT-large model takes four months. Hence, training big Transformers with long sequences (like n = 2048) will be expensive due to the O(n2) complexity.
Question 3: What is Nyströmformer? What’s its key approach?
Answer: Nyströmformer makes use of the approximation of the self-attention mechanism of BERT-small and BERT-base by adapting the Nyström approximation method in a way that the self-attention complexity is reduced to O(n) both in the sense of memory and time. In turn, it allows the model to support long sequences.
Figure 2 illustrates the proposed architecture of self-attention using the Nyström approximation. For a given input key (K) and query (Q), first, the model employs the Segment-means to compute landmark points as matrices K˜ and Q˜. In this process, n tokens are grouped into m segments, and then the mean of each segment is computed. The value of m is less than n.
The model then computes the Nyström approximation using the approximate Moore-Penrose pseudoinverse leveraging the landmark points. Moreover, a skip connection of value V, implemented using a 1D depthwise convolution (DConv box), is added to the model to help the training.
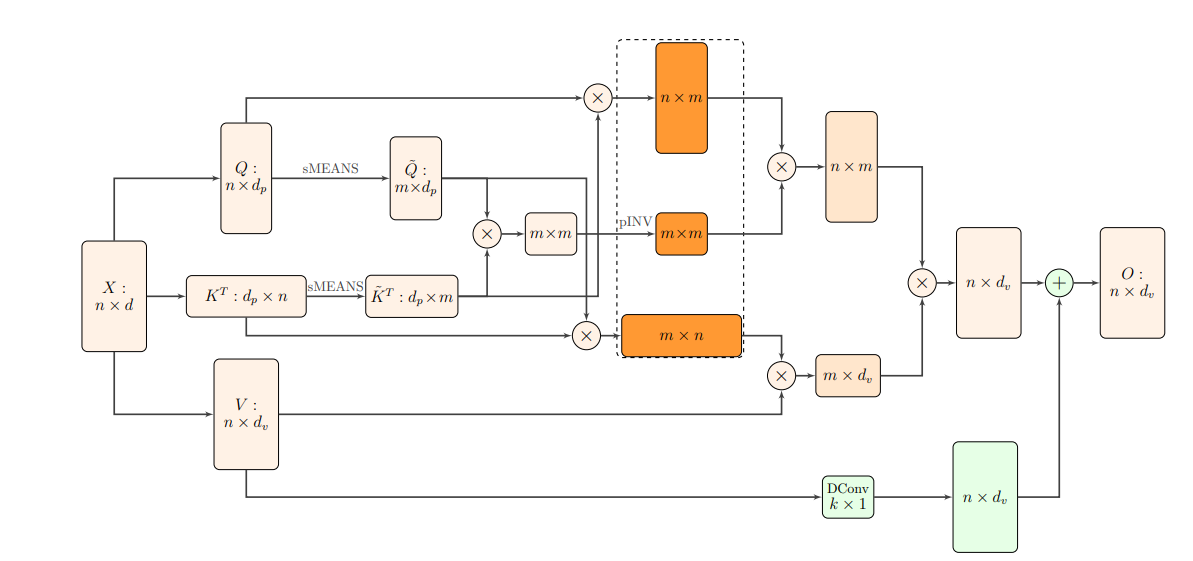
Figure 2: The proposed architecture of self-attention using Nyström approximation (Source: Arxiv)
This algorithm scales linearly w.r.t. the input sequence length (n) when the number of segments (m) is less than the sequence length (n) in the sense of both memory and time. Moreover, it retains the performance profile of other self-attention approximations but provides the added benefit of resource usage. It is a step towards building Transformer models on very long sequences.
Note: On experimenting, it was found that selecting just 32 or 64 landmarks yields competitive performance in comparison to standard self-attention and other effective attention techniques even for long sequence lengths, i.e., n=4096 or 8192.
Question 4: What is Nyström Method?
Answer: The Nyström method speeds up large-scale learning applications and decreases computational costs by producing low-rank approximations. Low-rank matrix approximations are crucial in applying kernel methods to large-scale learning problems.
The presumption that a matrix can be successfully approximated by using only a subset of its columns is essential to the effectiveness of this method.
In Nyströmformer, the Nyström method is used for matrix multiplication. It helps us to approximate a matrix by sampling the rows and columns. Specifically, for the given input key (K) and query (Q), the Nyströmformer model uses Segment-means to compute landmark points as matrices K˜ and Q˜.
Question 5: How was the Nyström method adapted to approximate self-attention?
So the key objective was to approximate the softmax matrix in standard self-attention, which is defined as follows:
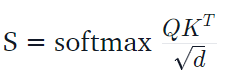
where Q and K are the queries and keys, respectively. As we partly discussed in Answer 3, m rows and columns are sampled from S, which form four sub-matrices, and S^ is obtained:
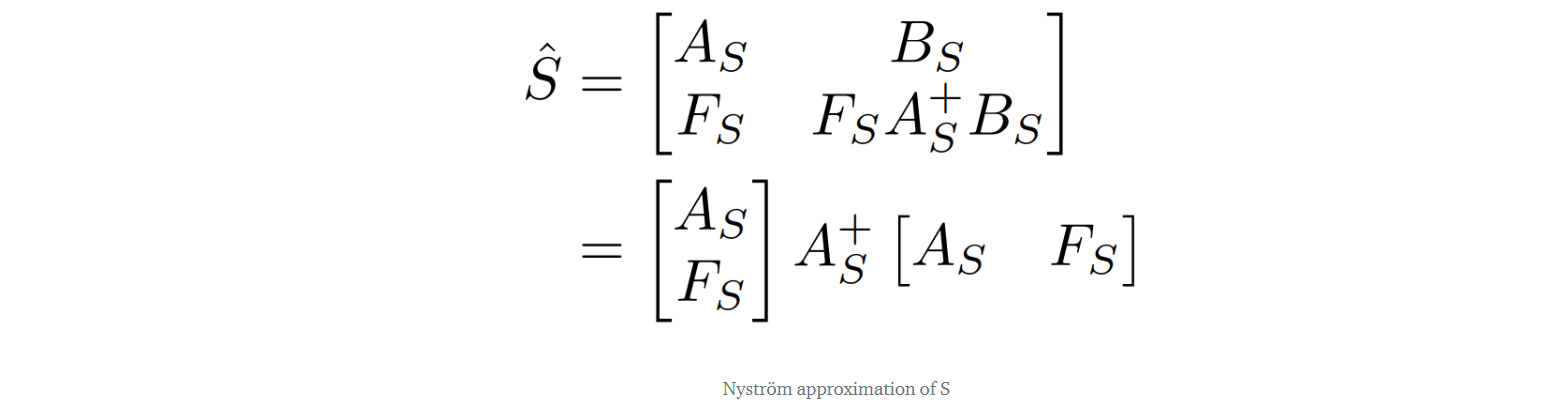
Later, the authors decided to sample landmarks (Q~ and K~) from queries (Q) and keys (K) rather than from S. Q~ and K~ are then used to construct three matrices that correspond to those in the Nyström approximation of S. The F~, A~, and, B~matrices are defined as follows:
The sizes of F~, A~, and, B~ are n×m, m×m, and m×n respectively. The new alternative Nyström approximation of the softmax matrix in the self-attention mechanism is defined as:
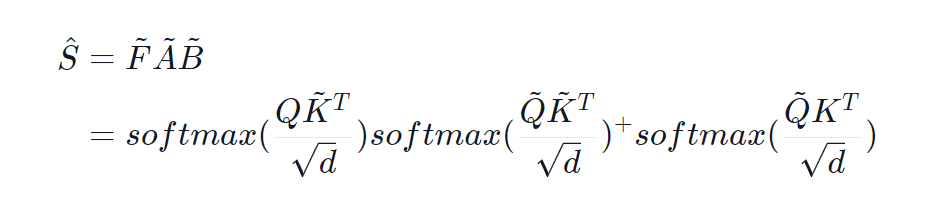
Then this matrix is multiplied by the values (V) to get a linear approximation of self-attention. Note that O(n2) complexity is avoided by never calculating the product QKT.
Figure 2 illustrates a Nyström approximation of the softmax matrix in self-attention. The left image displays the true softmax matrix used in self-attention, and the right image shows its Nyström approximation. Notably, the approximation is calculated by multiplying the three matrices we discussed.
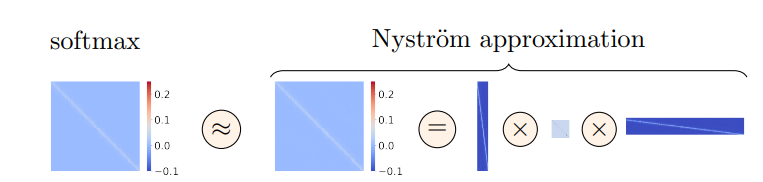
Figure 2: Nyström approximation of softmax matrix in self-attention. (Source: Arxiv)
The whole technique is further explained by Figure 3, which shows the pipeline for the Nyström approximation of softmax in self-attention.

Figure 3: Pipeline for Nyström approximation of softmax matrix in self-attention. (Source: Arxiv)
Note: The three orange matrices in figure 2 correspond to the three matrices we discussed in this answer.
Question 6: List some key achievements of Nyströmformer.
Following are some of the key achievements of Nyströmformer:
1. Evaluations on various downstream tasks on the GLUE benchmark and IMDB reviews with standard sequence length suggested that Nyströmformer performs comparably, or in some cases, even slightly better, than standard self-attention
2. Compared to other effective self-attention techniques, Nyströmformer performed well on longer sequence tasks in the Long Range Arena (LRA) benchmark.
Conclusion
This article covers some of the most imperative interview-winning questions on Nyströmformer that could be asked in data science interviews. Using these interview questions as a guide, you can not only improve your understanding of the fundamental concepts but also formulate effective answers and present them to the interviewer.
To sum it up, in this article, we explored the following:
- The main element that made it possible for transformers to work excellently was self-attention. It computes a weighted average of feature representations with the weight proportional to a similarity score between pairs of representations.
- Despite self-attention being beneficial, it is an efficiency bottleneck because it has a memory and time complexity of O(n2 ), where n is the length of an input sequence.
- Nyströmformer makes use of the approximation of the BERT-small and BERT-base self-attention mechanism by adapting the Nyström approximation in a way that the self-attention complexity is reduced to O(n) both in the sense of memory and time.
- Nystrom’s method minimizes computational costs by producing low-rank approximations.
The media shown in this article is not owned by Analytics Vidhya and is used at the Author’s discretion.




