This article was published as a part of the Data Science Blogathon.
Introduction
Time series forecasting is used to predict future values based on previously observed values and one of the best tools for trend analysis and future prediction.
What is time-series data?
It is recorded at regular time intervals, and the order of these data points is important. Therefore, any predictive model based on time series data will have time as an independent variable. The output of a model would be the predicted value or classification at a specific time.
Time series analysis vs time series forecasting
Let’s talk about some possible confusion about the Time Series Analysis and Forecasting. Time series forecasting is an example of predictive modeling whereas time series analysis is a form of descriptive modeling.
For a new investor general research which is associated with the stock or share market is not enough to make the decision. The common trend towards the stock market among the society is highly risky for investment so most of the people are not able to make decisions based on common trends. The seasonal variance and steady flow of any index will help both existing and new investors to understand and make a decision to invest in the share market.
To solve this kind of problem time series forecasting is the best technique.
Stock market
Stock markets are where individual and institutional investors come together to buy and sell shares in a public venue. Nowadays these exchanges exist as electronic marketplaces.
That supply and demand help determine the price for each security or the levels at which stock market participants — investors and traders — are willing to buy or sell.
The concept behind how the stock market works is pretty simple. Operating much like an auction house, the stock market enables buyers and sellers to negotiate prices and make trades.
Definition of ‘Stock’
A Stock or share (also known as a company’s “equity”) is a financial instrument that represents ownership in a company
Machine learning in the stock market
The stock market is very unpredictable, any geopolitical change can impact the share trend of stocks in the share market, recently we have seen how covid-19 has impacted the stock prices, which is why on financial data doing a reliable trend analysis is very difficult. The most efficient way to solve this kind of issue is with the help of Machine learning and Deep learning.
In this tutorial, we will be solving this problem with ARIMA Model.
A popular and widely used statistical method for time series forecasting is the ARIMA model. It is one of the most popular models to predict linear time series data. This model has been used extensively in the field of finance and economics as it is known to be robust, efficient, and has a strong potential for short-term share market prediction. Exponential smoothing and ARIMA models are the two most widely used approaches to time series forecasting and provide complementary approaches to the problem. While exponential smoothing models are based on a description of the trend and seasonality in the data, ARIMA models aim to describe the auto-correlation(Autocorrelation is the degree of similarity between a given time series and a lagged version of itself over successive time intervals) in the data.
To know about seasonality please refer to my previous blog, And to get a basic understanding of ARIMA I would recommend you to go through this blog, this will help you to get a better understanding of how Time Series analysis works.
Implementing stock price forecasting
I will be using nsepy library to extract the historical data for SBIN.
Imports and Reading Data
Python Code:
The data shows the stock price of SBIN from 2020-1-1 to 2020-11-1. The goal is to create a model that will forecast
the closing price of the stock.
Let us create a visualization which will show per day closing price of the stock-
plt.figure(figsize=(10,6))
plt.grid(True)
plt.xlabel('Dates')
plt.ylabel('Close Prices')
plt.plot(sbin['Close'])
plt.title('SBIN closing price')
plt.show()
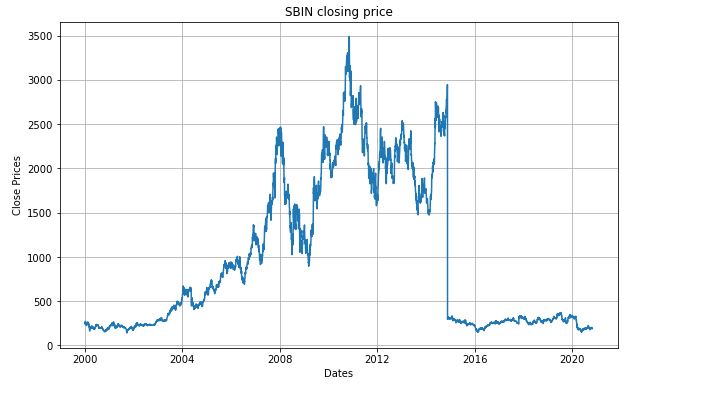
plt.figure(figsize=(10,6))
df_close = sbin['Close']
df_close.plot(style='k.')
plt.title('Scatter plot of closing price')
plt.show()
plt.figure(figsize=(10,6))
df_close = sbin['Close']
df_close.plot(style='k.',kind='hist')
plt.title('Hisogram of closing price')
plt.show()
First, we need to check if a series is stationary or not because time series analysis only works with stationary data.
Testing For Stationarity:
To identify the nature of the data, we will be using the null hypothesis.
H0: The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.
H1: The alternative hypothesis: It is a claim about the population that is contradictory to H0 and what we conclude when we reject H0.
If we fail to reject the null hypothesis, we can say that the series is non-stationary. This means that the series can be linear.
If both mean and standard deviation are flat lines(constant mean and constant variance), the series becomes stationary.
from statsmodels.tsa.stattools import adfuller
def test_stationarity(timeseries):
#Determing rolling statistics
rolmean = timeseries.rolling(12).mean()
rolstd = timeseries.rolling(12).std()
#Plot rolling statistics:
plt.plot(timeseries, color='yellow',label='Original')
plt.plot(rolmean, color='red', label='Rolling Mean')
plt.plot(rolstd, color='black', label = 'Rolling Std')
plt.legend(loc='best')
plt.title('Rolling Mean and Standard Deviation')
plt.show(block=False)
print("Results of dickey fuller test")
adft = adfuller(timeseries,autolag='AIC')
# output for dft will give us without defining what the values are.
#hence we manually write what values does it explains using a for loop
output = pd.Series(adft[0:4],index=['Test Statistics','p-value','No. of lags used','Number of observations used'])
for key,values in adft[4].items():
output['critical value (%s)'%key] = values
print(output)
test_stationarity(sbin['Close'])
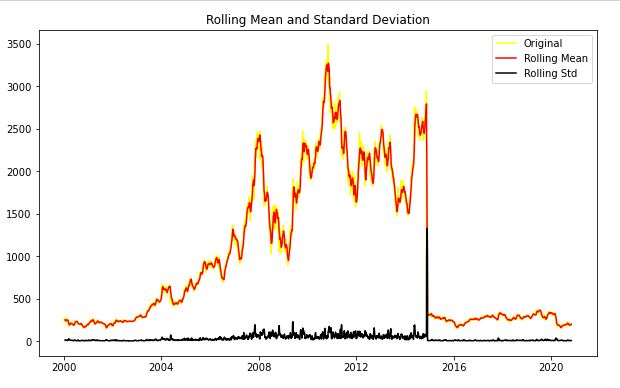
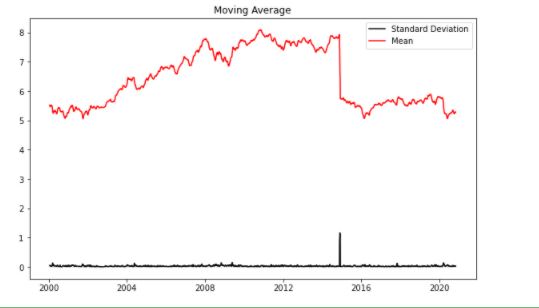
After analysing the above graph, we can see the increasing mean and standard deviation and hence our series is not stationary.
Results of dickey fuller test Test Statistics -1.914523 p-value 0.325260 No. of lags used 3.000000 Number of observations used 5183.000000 critical value (1%) -3.431612 critical value (5%) -2.862098 critical value (10%) -2.567067 dtype: float64
We see that the p-value is greater than 0.05 so we cannot reject the Null hypothesis. Also, the test statistics is greater than the critical values. so the data is non-stationary.
For time series analysis we separate Trend and Seasonality from the time series.
result = seasonal_decompose(df_close, model='multiplicative', freq = 30) fig = plt.figure() fig = result.plot() fig.set_size_inches(16, 9)
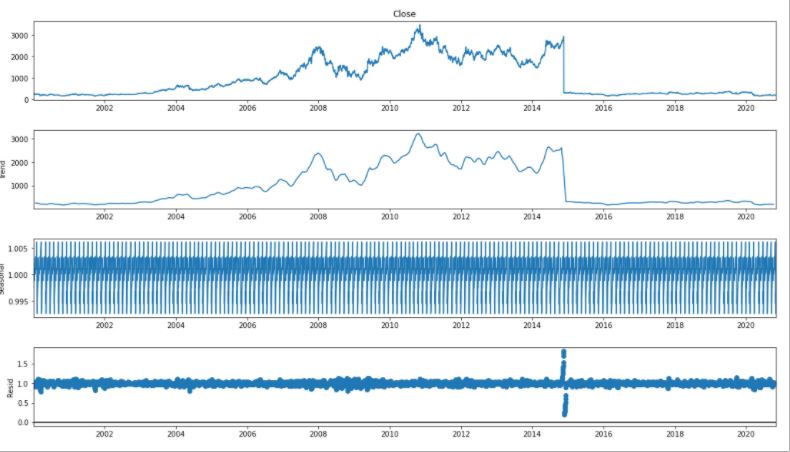
from pylab import rcParams
rcParams['figure.figsize'] = 10, 6
df_log = np.log(sbin['Close'])
moving_avg = df_log.rolling(12).mean()
std_dev = df_log.rolling(12).std()
plt.legend(loc='best')
plt.title('Moving Average')
plt.plot(std_dev, color ="black", label = "Standard Deviation")
plt.plot(moving_avg, color="red", label = "Mean")
plt.legend()
plt.show()
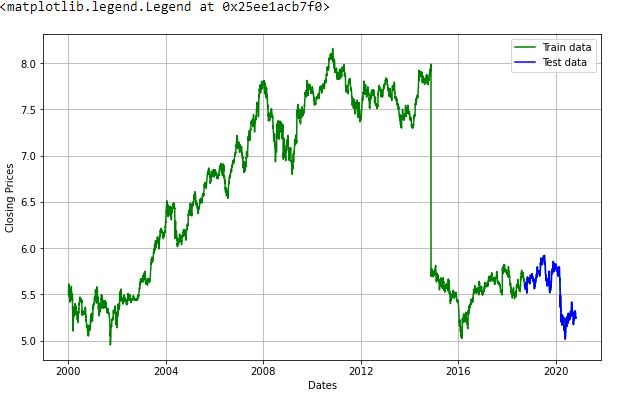
Now we are going to create an ARIMA model and will train it with the closing price of the stock on the train data. So let us split the data into training and test set and visualize it.
train_data, test_data = df_log[3:int(len(df_log)*0.9)], df_log[int(len(df_log)*0.9):]
plt.figure(figsize=(10,6))
plt.grid(True)
plt.xlabel('Dates')
plt.ylabel('Closing Prices')
plt.plot(df_log, 'green', label='Train data')
plt.plot(test_data, 'blue', label='Test data')
plt.legend()
model_autoARIMA = auto_arima(train_data, start_p=0, start_q=0, test='adf', # use adftest to find optimal 'd' max_p=3, max_q=3, # maximum p and q m=1, # frequency of series d=None, # let model determine 'd' seasonal=False, # No Seasonality start_P=0, D=0, trace=True, error_action='ignore', suppress_warnings=True, stepwise=True) print(model_autoARIMA.summary())
Performing stepwise search to minimize aic
ARIMA(0,1,0)(0,0,0)[0] intercept : AIC=-16607.561, Time=2.19 sec
ARIMA(1,1,0)(0,0,0)[0] intercept : AIC=-16607.961, Time=0.95 sec
ARIMA(0,1,1)(0,0,0)[0] intercept : AIC=-16608.035, Time=2.27 sec
ARIMA(0,1,0)(0,0,0)[0] : AIC=-16609.560, Time=0.39 sec
ARIMA(1,1,1)(0,0,0)[0] intercept : AIC=-16606.477, Time=2.77 sec
Best model: ARIMA(0,1,0)(0,0,0)[0]
Total fit time: 9.079 seconds
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 4665
Model: SARIMAX(0, 1, 0) Log Likelihood 8305.780
Date: Tue, 24 Nov 2020 AIC -16609.560
Time: 20:08:50 BIC -16603.113
Sample: 0 HQIC -16607.293
- 4665
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
sigma2 0.0017 1.06e-06 1566.660 0.000 0.002 0.002
===================================================================================
Ljung-Box (Q): 24.41 Jarque-Bera (JB): 859838819.58
Prob(Q): 0.98 Prob(JB): 0.00
Heteroskedasticity (H): 7.16 Skew: -37.54
Prob(H) (two-sided): 0.00 Kurtosis: 2105.12
===================================================================================
model_autoARIMA.plot_diagnostics(figsize=(15,8)) plt.show()
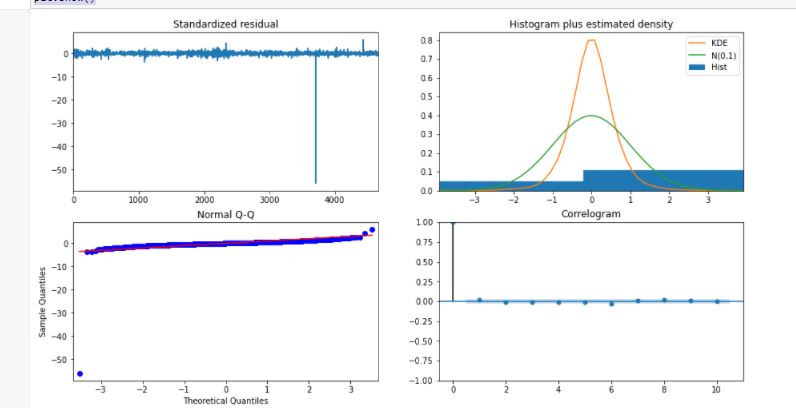
model = ARIMA(train_data, order=(3, 1, 2)) fitted = model.fit(disp=-1) print(fitted.summary())
ARIMA Model Results
==============================================================================
Dep. Variable: D.Close No. Observations: 4664
Model: ARIMA(3, 1, 2) Log Likelihood 8309.178
Method: css-mle S.D. of innovations 0.041
Date: Tue, 24 Nov 2020 AIC -16604.355
Time: 20:09:37 BIC -16559.222
Sample: 1 HQIC -16588.481
=================================================================================
coef std err z P>|z| [0.025 0.975]
---------------------------------------------------------------------------------
const 8.761e-06 0.001 0.015 0.988 -0.001 0.001
ar.L1.D.Close 1.3689 0.251 5.460 0.000 0.877 1.860
ar.L2.D.Close -0.7118 0.277 -2.567 0.010 -1.255 -0.168
ar.L3.D.Close 0.0094 0.021 0.445 0.657 -0.032 0.051
ma.L1.D.Close -1.3468 0.250 -5.382 0.000 -1.837 -0.856
ma.L2.D.Close 0.6738 0.282 2.391 0.017 0.122 1.226
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 0.9772 -0.6979j 1.2008 -0.0987
AR.2 0.9772 +0.6979j 1.2008 0.0987
AR.3 74.0622 -0.0000j 74.0622 -0.0000
MA.1 0.9994 -0.6966j 1.2183 -0.0969
MA.2 0.9994 +0.6966j 1.2183 0.0969
-----------------------------------------------------------------------------
# Forecast fc, se, conf = fitted.forecast(519, alpha=0.05) # 95% confidence
fc_series = pd.Series(fc, index=test_data.index)
lower_series = pd.Series(conf[:, 0], index=test_data.index)
upper_series = pd.Series(conf[:, 1], index=test_data.index)
plt.figure(figsize=(12,5), dpi=100)
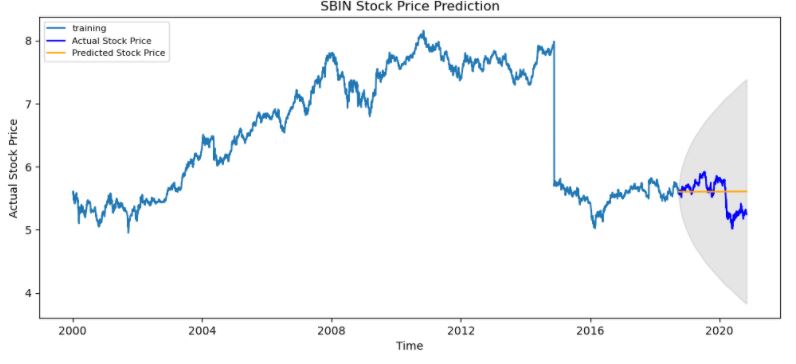
plt.plot(train_data, label='training')
plt.plot(test_data, color = 'blue', label='Actual Stock Price')
plt.plot(fc_series, color = 'orange',label='Predicted Stock Price')
plt.fill_between(lower_series.index, lower_series, upper_series,
color='k', alpha=.10)
plt.title('SBIN Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('Actual Stock Price')
plt.legend(loc='upper left', fontsize=8)
plt.show()
Conclusion
Time Series forecasting is really useful when we have to take future decisions or we have to do analysis, we can quickly do that using ARIMA, there are lots of other Models from we can do the time series forecasting but ARIMA is really easy to understand.
I hope this article will help you and save a good amount of time. Let me know if you have any suggestions.
HAPPY CODING.
Prabhat Pathak (Linkedin profile) is a Senior Analyst and innovation Enthusiast.




