Introduction
Most of us have limited knowledge of regression. Of which, linear and logistic regression are our favorite ones. As an interesting fact, regression has extended capabilities to deal with different types of variables. Do you know, regression has provisions for dealing with multi-level dependent variables too? I’m sure, you didn’t. Neither did I. Until I was pushed to explore this aspect of Regression.
For multi-level dependent variables, there are many machine learning algorithms which can do the job for you; such as naive Bayes, decision tree, random forest etc. For starters, these algorithm can be a bit difficult to understand. But, if you very well understand logistic regression, mastering this new aspect of regression should be easy for you!
In this article, I’ve explained the method of using multinomial and ordinal regression. Also, for practical purpose, I’ve demonstrated this algorithm in a step wise fashion in R. This article draws inspiration from a detailed article here . I have added my own take on it.
Note: This article is best suited for R users having prior knowledge of logistic regression. However, if you use python, you can still get a overall understanding of this regression method.
Table of contents
What is Multinomial Logistic Regression ?
Multinomial Logistic Regression (MLR) is a form of linear regression analysis conducted when the dependent variable is nominal with more than two levels. It is used to describe data and to explain the relationship between one dependent nominal variable and one or more continuous-level (interval or ratio scale) independent variables. You can understand nominal variable as, a variable which has no intrinsic ordering.
For example: Types of Forests: ‘Evergreen Forest’, ‘Deciduous Forest’, ‘Rain Forest’. As you see, there is no intrinsic order in them, but each forest represent a unique category. In other words, multinomial regression is an extension of logistic regression, which analyzes dichotomous (binary) dependents.
How does Multinomial Logistic Regression works ?
The multinomial logistic regression estimates a separate binary logistic regression model for each dummy variables. The result is M-1 binary logistic regression models. Each model conveys the effect of predictors on the probability of success in that category, in comparison to the reference category.
Each model has its own intercept and regression coefficients—the predictors can affect each category differently. Let’s compare this part with our classics – Linear and Logistic Regression.
Standard linear regression requires the dependent variable to be of continuous-level (interval or ratio) scale. However, logistic regression jumps the gap by assuming that the dependent variable is a stochastic event. And the dependent variable describes the outcome of this stochastic event with a density function (a function of cumulated probabilities ranging from 0 to 1).
Statisticians then argue one event happens if the probability is less than 0.5 and the opposite event happens when probability is greater than 0.5.
Now we know that MLR extends the binary logistic model to a model with numerous categories(in dependent variable). However, it has one limitation. The category to which an outcome belongs to, does not assume any order in it. For example, if we have N categories, all have an equal probability. In reality, we come across problems where categories have a natural order.
So, what to do when we have a natural order in categories of dependent variables ? In such situation, Ordinal Regression comes to our rescue.
What is Ordinal Logistic Regression ?
Ordinal Regression ( also known as Ordinal Logistic Regression) is another extension of binomial logistics regression. Ordinal regression is used to predict the dependent variable with ‘ordered’ multiple categories and independent variables. In other words, it is used to facilitate the interaction of dependent variables (having multiple ordered levels) with one or more independent variables.
For example: Let us assume a survey is done. We asked a question to respondent where their answer lies between agree or disagree. The responses thus collected didn’t help us to generalize well. Later, we added levels to our responses such as Strongly Disagree, Disagree, Agree, Strongly Agree.
This helped us to observe a natural order in the categories. For our regression model to be realistic, we must appreciate this order instead of being naive to it, as in the case of MLR. Ordinal Logistic Regression addresses this fact. Ordinal means order of the categories.
Examples
Before we perform these algorithm in R, let’s ensure that we have gained a concrete understanding using the cases below:
Case 1 (Multinomial Regression)
The modeling of program choices made by high school students can be done using Multinomial logit. The program choices are general program, vocational program and academic program. Their choice can be modeled using their writing score and their social economic status.
Based on a variety of attributes such as social status, channel type, awards and accolades received by the students, gender, economic status and how well they are able to read and write in the subjects given, the choice on the type of program can be predicted. Choice of programs with multiple levels (unordered) is the dependent variable. This case is suited for using Multinomial Logistic Regression technique.
Case 2 (Ordinal Regression)
A study looks at factors which influence the decision of whether to apply to graduate school. College juniors are asked if they are unlikely, somewhat likely, or very likely to apply to graduate school. Hence, our outcome variable has three categories i.e. unlikely, somewhat likely and very likely.
Data on parental educational status, class of institution (private or state run), current GPA are also collected. The researchers have reason to believe that the “distances” between these three points are not equal. For example, the “distance” between “unlikely” and “somewhat likely” may be shorter than the distance between “somewhat likely” and “very likely”. In such case, we’ll use Ordinal Regression.
Multinomial Logistic Regression (MLR) in R
Read the file
> library("foreign")
> ml <- read.dta("http://www.ats.ucla.edu/stat/data/hsbdemo.dta")Re-leveling data
> head(ml)
## id female ses schtyp prog read write math science socst ## 1 45 female low public vocation 34 35 41 29 26 ## 2 108 male middle public general 34 33 41 36 36 ## 3 15 male high public vocation 39 39 44 26 42 ## 4 67 male low public vocation 37 37 42 33 32 ## 5 153 male middle public vocation 39 31 40 39 51 ## 6 51 female high public general 42 36 42 31 39 ## honors awards cid ## 1 not enrolled 0 1 ## 2 not enrolled 0 1 ## 3 not enrolled 0 1 ## 4 not enrolled 0 1 ## 5 not enrolled 0 1 ## 6 not enrolled 0 1
> ml$prog2 <- relevel(ml$prog, ref = "academic")
Now we’ll execute a multinomial regression with two independent variable.
> library("nnet")
> test <- multinom(prog2 ~ ses + write, data = ml)## # weights: 15 (8 variable)
## initial value 219.722458
## iter 10 value 179.982880
## final value 179.981726
## converged> summary(test)
## Call:
## multinom(formula = prog2 ~ ses + write, data = ml)
##
## Coefficients:
## (Intercept) sesmiddle seshigh write
## general 2.852198 -0.5332810 -1.1628226 -0.0579287
## vocation 5.218260 0.2913859 -0.9826649 -0.1136037
##
## Std. Errors:
## (Intercept) sesmiddle seshigh write
## general 1.166441 0.4437323 0.5142196 0.02141097
## vocation 1.163552 0.4763739 0.5955665 0.02221996
##
## Residual Deviance: 359.9635
## AIC: 375.9635Interpretation
1. Model execution output shows some iteration history and includes the final negative log-likelihood 179.981726. This value is multiplied by two as shown in the model summary as the Residual Deviance.
2. The summary output has a block of coefficients and another block of standard errors. Each blocks has one row of values corresponding to one model equation. In the block of coefficients, we see that the first row is being compared to prog = “general” to our baseline prog = “academic” and the second row to prog = “vocation” to our baseline prog = “academic”.
3. A one-unit increase in write decreases the log odds of being in general program vs. academic program by 0.0579
4. A one-unit increase in write decreases the log odds of being in vocation program vs. academic program by 0.1136
5. The log odds of being in general program than in academic program will decrease by 1.163 if moving from ses=”low” to ses=”high”.
6. On the other hand, Log odds of being in general program than in academic program will decrease by 0.5332 if moving from ses=”low” to ses=”middle”
7. The log odds of being in vocation program vs. in academic program will decrease by 0.983 if moving from ses=”low” to ses=”high”
8. The log odds of being in vocation program vs. in academic program will increase by 0.291 if moving from ses=”low” to ses=”middle”
Now we’ll calculate Z score and p-Value for the variables in the model.
> z <- summary(test)$coefficients/summary(test)$standard.errors
> z## (Intercept) sesmiddle seshigh write ## general 2.445214 -1.2018081 -2.261334 -2.705562 ## vocation 4.484769 0.6116747 -1.649967 -5.112689
> p <- (1 - pnorm(abs(z), 0, 1))*2
> p## (Intercept) sesmiddle seshigh write ## general 0.0144766100 0.2294379 0.02373856 6.818902e-03 ## vocation 0.0000072993 0.5407530 0.09894976 3.176045e-07
> exp(coef(test))## (Intercept) sesmiddle seshigh write ## general 17.32582 0.5866769 0.3126026 0.9437172 ## vocation 184.61262 1.3382809 0.3743123 0.8926116
The p-Value tells us that ses variables are not significant. Now we’ll explore the entire data set, and analyze if we can remove any variables which do not add to model performance.
> names(ml)## [1] "id" "female" "ses" "schtyp" "prog" "read" "write" ## [8] "math" "science" "socst" "honors" "awards" "cid" "prog2"
> levels(ml$female)## [1] "male" "female"
> levels(ml$ses)
## [1] "low" "middle" "high"
> levels(ml$schtyp)## [1] "public" "private"
> levels(ml$honors)
## [1] "not enrolled" "enrolled"
Let’s now build a multinomial model on the entire data set after removing id and prog variables.
> test <- multinom(prog2 ~ ., data = ml[,-c(1,5,13)])## # weights: 39 (24 variable) ## initial value 219.722458 ## iter 10 value 178.757016 ## iter 20 value 155.866327 ## iter 30 value 154.365307 ## final value 154.365305 ## converged
> summary(test)## Call: ## multinom(formula = prog2 ~ ., data = ml[, -c(1, 5, 13)]) ## ## Coefficients: ## (Intercept) femalefemale sesmiddle seshigh schtypprivate ## general 5.692368 0.1547445 -0.2809824 -0.9632924107 -0.5872049 ## vocation 9.839107 0.4076641 1.2246933 0.0008659972 -1.9089941 ## read write math science socst ## general -0.04421300 -0.05434029 -0.1001477 0.10397170 -0.02486526 ## vocation -0.04124332 -0.05149742 -0.1209839 0.06341246 -0.07012002 ## honorsenrolled awards ## general -0.5963679 0.26104317 ## vocation 1.0986972 -0.08573852 ## ## Std. Errors: ## (Intercept) femalefemale sesmiddle seshigh schtypprivate ## general 2.385383 0.4514339 0.5224132 0.5934146 0.5597181 ## vocation 2.566895 0.4993567 0.5764471 0.6885407 0.8313621 ## read write math science socst ## general 0.03076523 0.05109711 0.03514069 0.03153073 0.02697888 ## vocation 0.03451435 0.05358824 0.03902319 0.03252487 0.02912126 ## honorsenrolled awards ## general 0.8708913 0.2969302 ## vocation 0.9798571 0.3708768 ## ## Residual Deviance: 308.7306 ## AIC: 356.7306
Let’s check for fitted values now.
> head(fitted(test))## academic general vocation ## 1 0.08952937 0.1811189 0.7293518 ## 2 0.05219222 0.1229310 0.8248768 ## 3 0.54704495 0.0849831 0.3679719 ## 4 0.17103536 0.2750466 0.5539180 ## 5 0.10014015 0.2191946 0.6806652 ## 6 0.27287474 0.1129348 0.6141905
Once we have build the model, we’ll use it for prediction. Let us create a new data set with different permutation and combinations.
> expanded=expand.grid(female=c("female", "male", "male", "male"), ses=c("low","low","middle", "high"), schtyp=c("public", "public", "private", "private"), read=c(20,50,60,70), write=c(23,45,55,65), math=c(30,46,76,54), science=c(25,45,68,51), socst=c(30, 35, 67, 61), honors=c("not enrolled", "not enrolled", "enrolled","not enrolled"), awards=c(0,0,3,0,6) )
> head(expanded)
## female ses schtyp read write math science socst honors awards ## 1 female low public 20 23 30 25 30 not enrolled 0 ## 2 male low public 20 23 30 25 30 not enrolled 0 ## 3 male low public 20 23 30 25 30 not enrolled 0 ## 4 male low public 20 23 30 25 30 not enrolled 0 ## 5 female low public 20 23 30 25 30 not enrolled 0 ## 6 male low public 20 23 30 25 30 not enrolled 0
> predicted=predict(test,expanded,type="probs")
> head(predicted)## academic general vocation ## 1 0.01357216 0.1759060 0.8105219 ## 2 0.01929452 0.2142205 0.7664850 ## 3 0.01929452 0.2142205 0.7664850 ## 4 0.01929452 0.2142205 0.7664850 ## 5 0.01357216 0.1759060 0.8105219 ## 6 0.01929452 0.2142205 0.7664850
Now, we’ll calculate the prediction values. The parameter type=”probs”, specifies our interest in probabilities. In order to plot predicted probabilities for intuitive understanding, we add predicted probability values to data.
> bpp=cbind(expanded, predicted)Now we’ll calculate the mean probabilities within each level of ses.
> by(bpp[,4:7], bpp$ses, colMeans)
## bpp$ses: low ## read write math science ## 50.00 47.00 51.50 47.25 ## -------------------------------------------------------- ## bpp$ses: middle ## read write math science ## 50.00 47.00 51.50 47.25 ## -------------------------------------------------------- ## bpp$ses: high ## read write math science ## 50.00 47.00 51.50 47.25
I’ve used the melt() function from ‘reshape2’ package. It “melts” data with the purpose of each row being a unique id-variable combination.
> library("reshape2")## Warning: package 'reshape2' was built under R version 3.1.3> bpp2 = melt (bpp,id.vars=c("female", "ses","schtyp", "read","write","math","science","socst","honors", "awards"),value.name="probablity")> head(bpp2)
## female ses schtyp read write math science socst honors awards ## 1 female low public 20 23 30 25 30 not enrolled 0 ## 2 male low public 20 23 30 25 30 not enrolled 0 ## 3 male low public 20 23 30 25 30 not enrolled 0 ## 4 male low public 20 23 30 25 30 not enrolled 0 ## 5 female low public 20 23 30 25 30 not enrolled 0 ## 6 male low public 20 23 30 25 30 not enrolled 0 ## variable probablity ## 1 academic 0.01357216 ## 2 academic 0.01929452 ## 3 academic 0.01929452 ## 4 academic 0.01929452 ## 5 academic 0.01357216 ## 6 academic 0.01929452
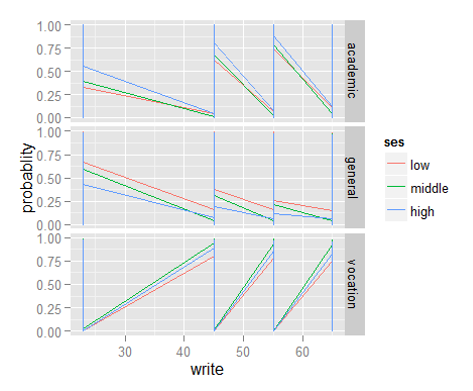
Now, we will be plotting graphs to explore the distribution of dependent variable vs independent variables, using ggplot() function. In ggplot, the first parameter in this function is the data values to be plotted. The second part is where (aes()) binds variables to x and y axis. We tell the plotting function to draw a line using geom_line(). We are differentiating the school type by plotting them in different colors.
> library("ggplot2")> ggplot(bpp2, aes(x = write, y = probablity, colour = ses)) +
geom_line() + facet_grid(variable ~ ., scales="free")Till here, we have learnt to use multinomial regression in R. As mentioned above, if you have prior knowledge of logistic regression, interpreting the results wouldn’t be too difficult. Let’s now proceed to understand ordinal regression in R.
Ordinal Logistic Regression (OLR) in R
Below are the steps to perform OLR in R:
Load the Libraries
> require(foreign)
> require(ggplot2)
> require(MASS)
> require(Hmisc)
> require(reshape2)
Load the data
> dat <- read.dta("http://www.ats.ucla.edu/stat/data/ologit.dta")> head(dat)
## apply pared public gpa ## 1 very likely 0 0 3.26 ## 2 somewhat likely 1 0 3.21 ## 3 unlikely 1 1 3.94 ## 4 somewhat likely 0 0 2.81 ## 5 somewhat likely 0 0 2.53 ## 6 unlikely 0 1 2.59
Let’s quickly understand the data.
The data set has a dependent variable known as apply. It has 3 levels namely “unlikely”, “somewhat likely”, and “very likely”, coded in 1, 2, and 3 respectively. 3 being highest and 1 being lowest. This situation is best for using ordinal regression because of presence of ordered categories. Pared (0/1) refers to at least one parent has a graduate degree; public (0/1) refers to the type of undergraduate institute.
For building this model, we will be using the polr command to estimate an ordered logistic regression. Then, we’ll specify Hess=TRUE to let the model output show the observed information matrix from optimization which is used to get standard errors.
> m <- polr(apply ~ pared + public + gpa, data = dat, Hess=TRUE)> summary(m)
## Call: ## polr(formula = apply ~ pared + public + gpa, data = dat, Hess = TRUE) ## ## Coefficients: ## Value Std. Error t value ## pared 1.04769 0.2658 3.9418 ## public -0.05879 0.2979 -0.1974 ## gpa 0.61594 0.2606 2.3632 ## ## Intercepts: ## Value Std. Error t value ## unlikely|somewhat likely 2.2039 0.7795 2.8272 ## somewhat likely|very likely 4.2994 0.8043 5.3453 ## ## Residual Deviance: 717.0249 ## AIC: 727.0249
We see the usual regression output coefficient table including the value of each coefficient, standard errors, t values, estimates for the two intercepts, residual deviance and AIC. AIC is the information criteria. Lesser the better.
Now we’ll calculate some essential metrics such as p-Value, CI, Odds ratio
> ctable <- coef(summary(m))
## Value Std. Error t value ## pared 1.04769010 0.2657894 3.9418050 ## public -0.05878572 0.2978614 -0.1973593 ## gpa 0.61594057 0.2606340 2.3632399 ## unlikely|somewhat likely 2.20391473 0.7795455 2.8271792 ## somewhat likely|very likely 4.29936315 0.8043267 5.3452947
> p <- pnorm(abs(ctable[, "t value"]), lower.tail = FALSE) * 2> ctable <- cbind(ctable, "p value" = p)
## Value Std. Error t value p value ## pared 1.04769010 0.2657894 3.9418050 8.087072e-05 ## public -0.05878572 0.2978614 -0.1973593 8.435464e-01 ## gpa 0.61594057 0.2606340 2.3632399 1.811594e-02 ## unlikely|somewhat likely 2.20391473 0.7795455 2.8271792 4.696004e-03 ## somewhat likely|very likely 4.29936315 0.8043267 5.3452947 9.027008e-08
# confidence intervals> ci <- confint(m)
## Waiting for profiling to be done...
## 2.5 % 97.5 % ## pared 0.5281768 1.5721750 ## public -0.6522060 0.5191384 ## gpa 0.1076202 1.1309148
> exp(coef(m))
## pared public gpa ## 2.8510579 0.9429088 1.8513972
## OR and CI> exp(cbind(OR = coef(m), ci))
## OR 2.5 % 97.5 % ## pared 2.8510579 1.6958376 4.817114 ## public 0.9429088 0.5208954 1.680579 ## gpa 1.8513972 1.1136247 3.098490
Interpretation
1. One unit increase in parental education, from 0 (Low) to 1 (High), the odds of “very likely” applying versus “somewhat likely” or “unlikely” applying combined are 2.85 greater .
2. The odds “very likely” or “somewhat likely” applying versus “unlikely” applying is 2.85 times greater .
3. For gpa, when a student’s gpa moves 1 unit, the odds of moving from “unlikely” applying to “somewhat likely” or “very likley” applying (or from the lower and middle categories to the high category) are multiplied by 1.85.
Let’s now try to enhance this model to obtain better prediction estimates.
> summary(m)
## Call:
## polr(formula = apply ~ pared + public + gpa, data = dat, Hess = TRUE)
##
## Coefficients:
## Value Std. Error t value
## pared 1.04769 0.2658 3.9418
## public -0.05879 0.2979 -0.1974
## gpa 0.61594 0.2606 2.3632
##
## Intercepts:
## Value Std. Error t value
## unlikely|somewhat likely 2.2039 0.7795 2.8272
## somewhat likely|very likely 4.2994 0.8043 5.3453
##
## Residual Deviance: 717.0249
## AIC: 727.0249> summary(update(m, method = "probit", Hess = TRUE), digits = 3)
## Call:
## polr(formula = apply ~ pared + public + gpa, data = dat, Hess = TRUE,
## method = "probit")
##
## Coefficients:
## Value Std. Error t value
## pared 0.5981 0.158 3.7888
## public 0.0102 0.173 0.0588
## gpa 0.3582 0.157 2.2848
##
## Intercepts:
## Value Std. Error t value
## unlikely|somewhat likely 1.297 0.468 2.774
## somewhat likely|very likely 2.503 0.477 5.252
##
## Residual Deviance: 717.4951
## AIC: 727.4951> summary(update(m, method = "logistic", Hess = TRUE), digits = 3)
## Call:
## polr(formula = apply ~ pared + public + gpa, data = dat, Hess = TRUE,
## method = "logistic")
##
## Coefficients:
## Value Std. Error t value
## pared 1.0477 0.266 3.942
## public -0.0588 0.298 -0.197
## gpa 0.6159 0.261 2.363
##
## Intercepts:
## Value Std. Error t value
## unlikely|somewhat likely 2.204 0.780 2.827
## somewhat likely|very likely 4.299 0.804 5.345
##
## Residual Deviance: 717.0249
## AIC: 727.0249> summary(update(m, method = "cloglog", Hess = TRUE), digits = 3)
## Call:
## polr(formula = apply ~ pared + public + gpa, data = dat, Hess = TRUE,
## method = "cloglog")
##
## Coefficients:
## Value Std. Error t value
## pared 0.517 0.161 3.202
## public 0.108 0.168 0.643
## gpa 0.334 0.154 2.168
##
## Intercepts:
## Value Std. Error t value
## unlikely|somewhat likely 0.871 0.455 1.912
## somewhat likely|very likely 1.974 0.461 4.287
##
## Residual Deviance: 719.4982
## AIC: 729.4982Let’s add interaction terms here.
> head(predict(m, dat, type = “p”))
## unlikely somewhat likely very likely
## 1 0.5488310 0.3593310 0.09183798
## 2 0.3055632 0.4759496 0.21848725
## 3 0.2293835 0.4781951 0.29242138
## 4 0.6161224 0.3126888 0.07118879
## 5 0.6560149 0.2833901 0.06059505
## 6 0.6609240 0.2797117 0.05936430> addterm(m, ~.^2, test = "Chisq")
## Single term additions
##
## Model:
## apply ~ pared + public + gpa
## Df AIC LRT Pr(Chi)
## <none> 727.02
## pared:public 1 727.81 1.21714 0.2699
## pared:gpa 1 728.98 0.04745 0.8276
## public:gpa 1 728.60 0.42953 0.5122> m2 <- stepAIC(m, ~.^2)> m2
## Start: AIC=727.02
## apply ~ pared + public + gpa
##
## Df AIC
## - public 1 725.06
## <none> 727.02
## + pared:public 1 727.81
## + public:gpa 1 728.60
## + pared:gpa 1 728.98
## - gpa 1 730.67
## - pared 1 740.60
##
## Step: AIC=725.06
## apply ~ pared + gpa
##
## Df AIC
## <none> 725.06
## + pared:gpa 1 727.02
## + public 1 727.02
## - gpa 1 728.79
## - pared 1 738.60> summary(m2)
## Call:
## polr(formula = apply ~ pared + gpa, data = dat, Hess = TRUE)
##
## Coefficients:
## Value Std. Error t value
## pared 1.0457 0.2656 3.937
## gpa 0.6042 0.2539 2.379
##
## Intercepts:
## Value Std. Error t value
## unlikely|somewhat likely 2.1763 0.7671 2.8370
## somewhat likely|very likely 4.2716 0.7922 5.3924
##
## Residual Deviance: 717.0638
## AIC: 725.0638> m2$anova
## Stepwise Model Path
## Analysis of Deviance Table
##
## Initial Model:
## apply ~ pared + public + gpa
##
## Final Model:
## apply ~ pared + gpa
##
##
## Step Df Deviance Resid. Df Resid. Dev AIC
## 1 395 717.0249 727.0249
## 2 - public 1 0.03891634 396 717.0638 725.0638> anova(m, m2)
## Likelihood ratio tests of ordinal regression models
##
## Response: apply
## Model Resid. df Resid. Dev Test Df LR stat.
## 1 pared + gpa 396 717.0638
## 2 pared + public + gpa 395 717.0249 1 vs 2 1 0.03891634
## Pr(Chi)
## 1
## 2 0.8436145Time to plot this model.
> m3 <- update(m, Hess=TRUE)> pr <- profile(m3)> confint(pr)
## 2.5 % 97.5 % ## pared 0.5281772 1.5721695 ## public -0.6522008 0.5191415 ## gpa 0.1076189 1.1309092
> plot(pr)
> pairs(pr)
Conclusion
I enjoyed writing this article. I’d suggest you to pay attention to interpretation aspect of the model. Coding is relatively easy, but unless you know what’s resulting, you learning will be incomplete.
There are many essential factors such as AIC, Residuals values to determine the effectiveness of the model. If you still struggle to understand them, I’d suggest you to brush your Basics of Logistic Regression. This should help you in understanding this concept better.
In this article, I shared my understanding of using multinomial and ordinal regression in R. These techniques are used when the dependent variable has levels either ordered or unordered.
Did you find this article helpful ? Have you used this technique to build any models ? Do share your experience and suggestions in the comments section below.
Frequently Asked Questions
A. Multinomial logistic regression is used to model the relationship between a categorical dependent variable with more than two categories and one or more independent variables. It can be applied in a variety of fields such as predicting customer behavior, medical research, political science, and image classification. The goal is to predict the probability of each category of the dependent variable based on the values of the independent variables.
A. Logistic regression is used to model the relationship between a binary dependent variable and one or more independent variables, whereas multinomial logistic regression is used for modeling the relationship between a categorical dependent variable with more than two categories and one or more independent variables. Logistic regression predicts the probability of one outcome, while multinomial logistic regression predicts the probability of multiple outcomes simultaneously.
A. Ordinal logistic regression is a statistical method used to analyze the relationship between an ordinal dependent variable (a variable with ordered categories, such as “low,” “medium,” and “high”) and one or more independent variables. It can be used to model outcomes such as satisfaction levels or grades. The goal is to predict the probability of an observation belonging to a certain category or a higher category, based on the values of the independent variables.
About the Author
Sray Agarwal is the chief manager of Bennett Coleman and Co. Ltd. (Times Group) and works as Subject Matter Expert (SME) for Business Analytics program. He has more than 8.5 years of experience in data science and BA.
He holds a degree in Business Analytics from Indian School of Business (ISB), Hyderabad. and graduated with an award of Academic Excellence and has been the part of the Dean’s List. Along with this he is a SAS certified Predictive Modeller.
If you like what you just read & want to continue your analytics learning, subscribe to our emails, follow us on twitter or like our facebook page.