Guide to the Intuitive Confusion Matrix

Introduction to Confusion Matrix

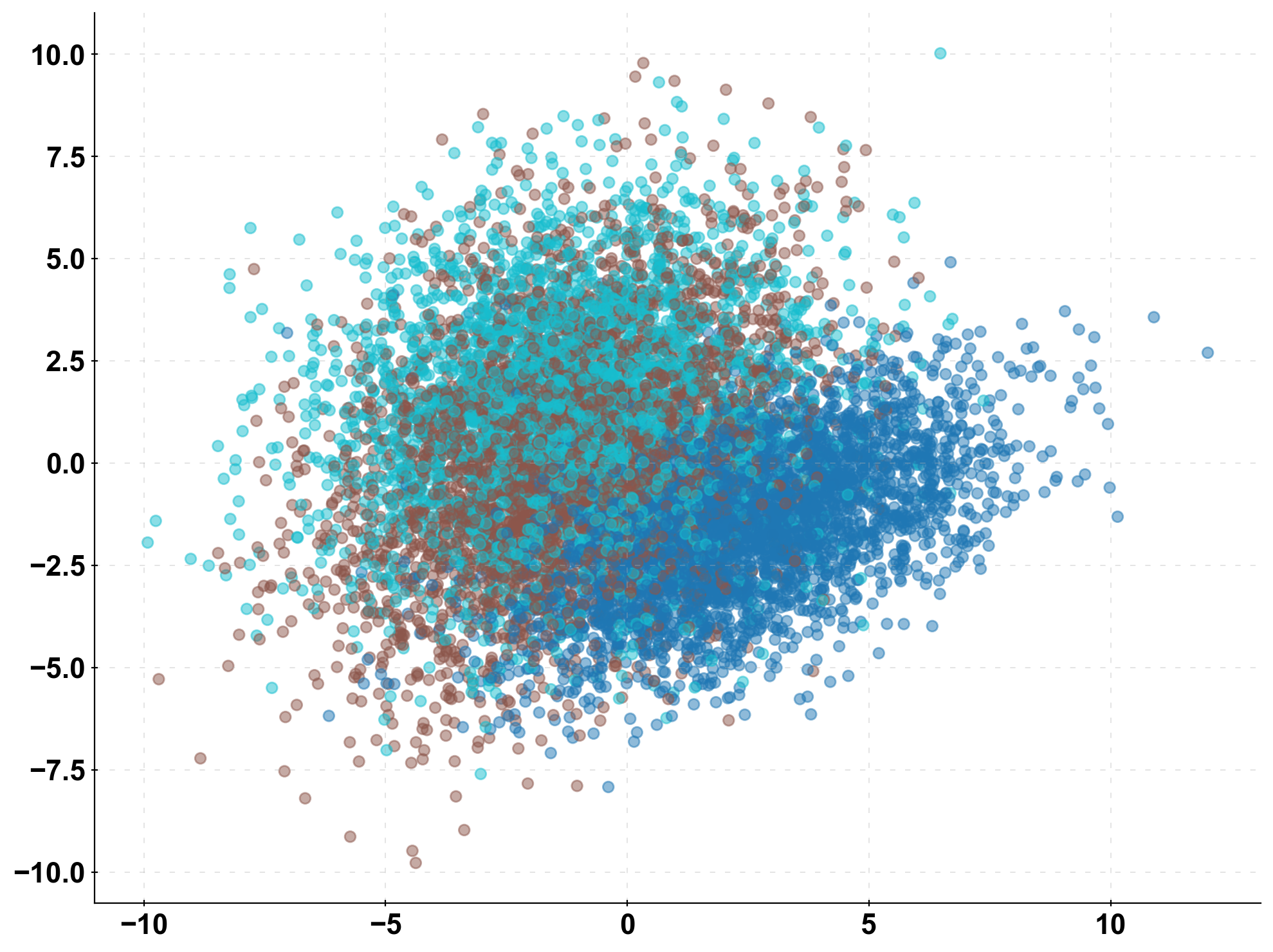
Houston, we need a Problem!

# generate the data and make predictions with our two models
n_classes = 3
X, y = make_classification(n_samples=10000, n_features=10,
                           n_classes=n_classes, n_clusters_per_class=1,
                           n_informative=10, n_redundant=0)
y = y.astype(int)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=0)
prediction_naive = np.random.randint(low=0, high=n_classes, size=len(y_test))
clf = LogisticRegression().fit(X_train, y_train)
prediction = clf.predict(X_test)

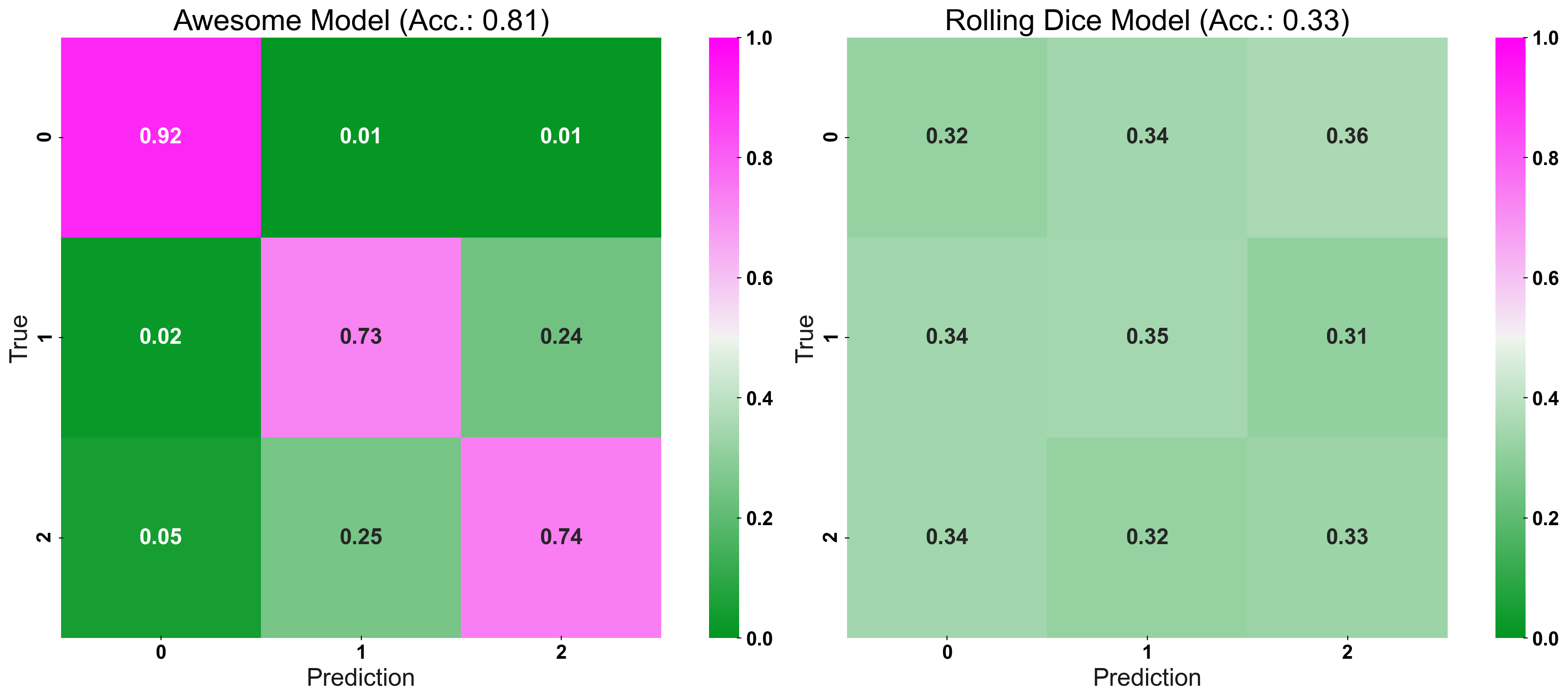
The Standard Confusion Matrix

fig, (ax1, ax2) = plt.subplots(1,2, figsize=(20,8))

plot_cm_standard(y_true=y_test, y_pred=prediction, title="Awesome Model", list_classes=[str(i) for i in range(n_classes)],

normalize="prediction", ax=ax1)

plot_cm_standard(y_true=y_test, y_pred=prediction_naive, title="Rolling Dice Model", list_classes=[str(i) for i in range(n_classes)],

normalize="prediction", ax=ax2)

plt.show()

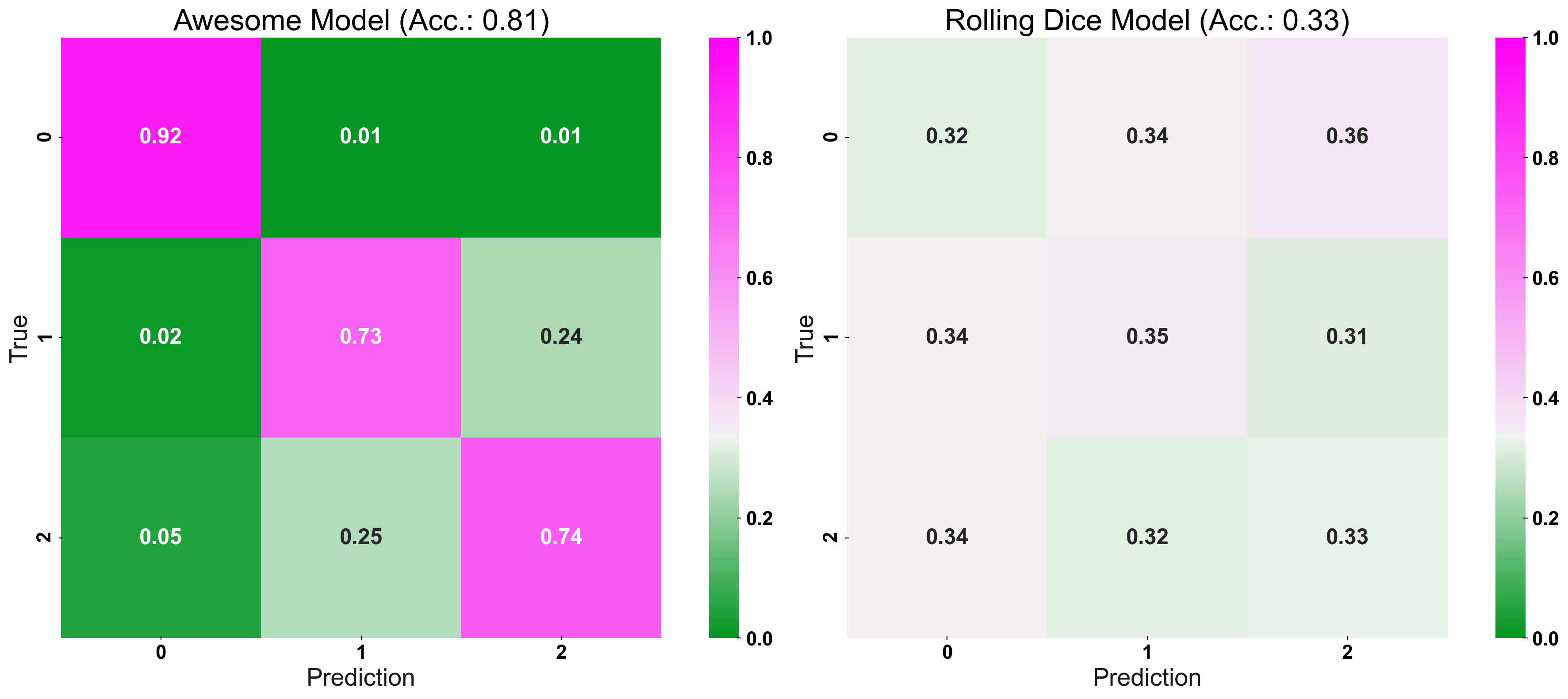
Now, we enter the secret sauce: CM_Norm adjusts the colour-bar, such that its point of origin is equal to the accuracy expected for a random prediction. Essentially, the “naive-prediction accuracy” is our “point of origin” because a model which predicts worse than a coin-flip, is not a helpful model to begin with (hence the name: “coin-flip confusion-matrix”). In other words, we are interested in a models “excess performance”, rather than its “absolute” error rates. To give two examples: For 3 different classes, the “point of origin”, of the colour-bar, would be set at 1/3, or for 10 classes it would be set at 1/10.

Strong Colours Equal a Strong Model!

fig, (ax1, ax2) = plt.subplots(1,2, figsize=(20,8))

plot_cm(y_true=y_test, y_pred=prediction, title="Awesome Model", list_classes=[str(i) for i in range(n_classes)],

normalize="prediction", ax=ax1)

plot_cm(y_true=y_test, y_pred=prediction_naive, title="Rolling Dice Model", list_classes=[str(i) for i in range(n_classes)],

normalize="prediction", ax=ax2)

plt.show()

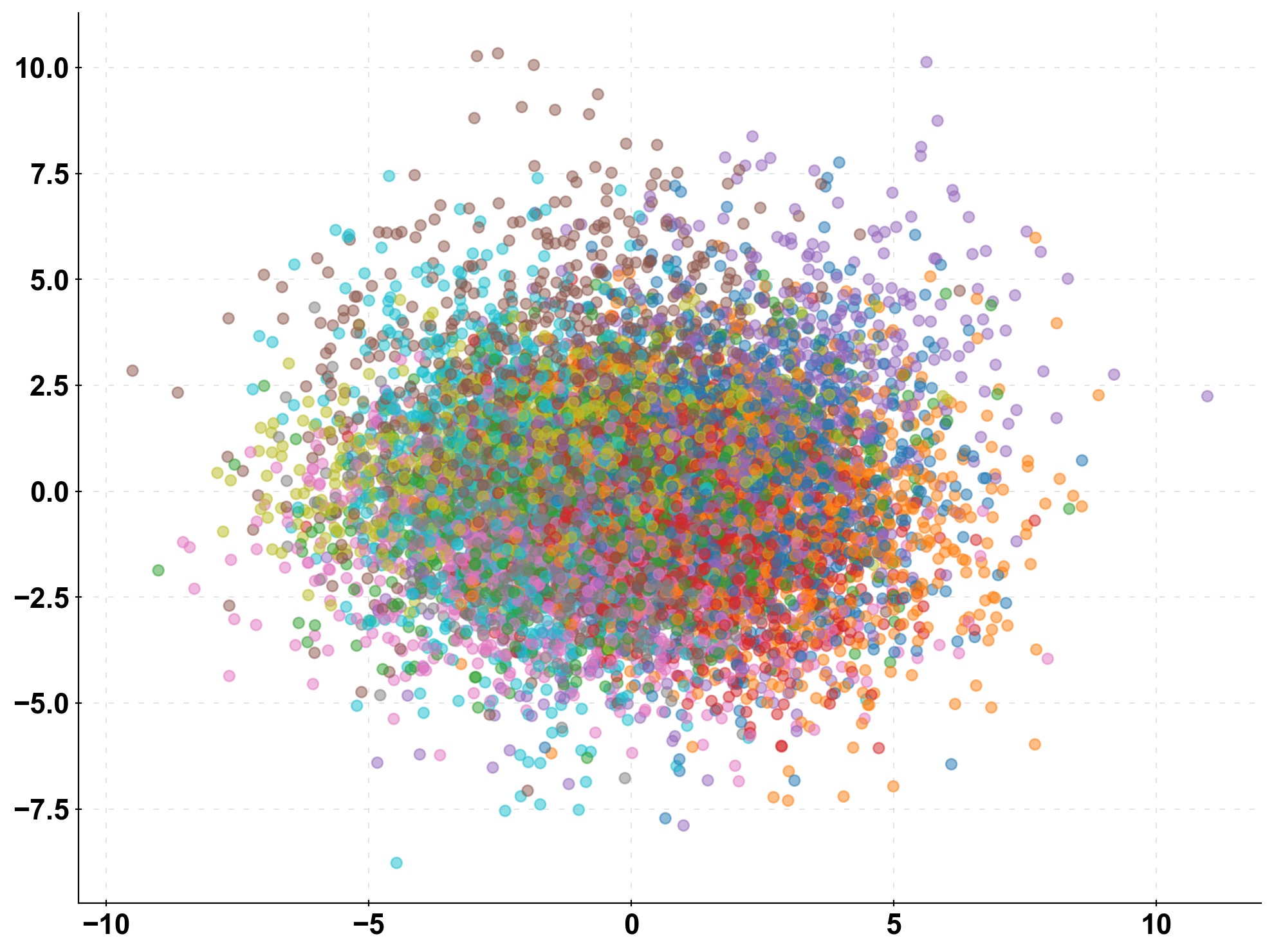
Dial-up the Complexity

n_classes = 10

X, y = make_classification(n_samples=10000, n_features=10,

n_classes=n_classes, n_clusters_per_class=1,

n_informative=10, n_redundant=0)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=0)

prediction_naive = np.random.randint(low=0, high=n_classes, size=len(y_test))

clf = LogisticRegression().fit(X_train, y_train)

prediction = clf.predict(X_test)

fig, (ax1, ax2) = plt.subplots(1,2, figsize=(20,8))
plot_cm_standard(y_true=y_test, y_pred=prediction, title="Awesome Model", list_classes=[str(i) for i in range(n_classes)],
        normalize="prediction", ax=ax1)
plot_cm_standard(y_true=y_test, y_pred=prediction_naive, title="Rolling Dice Model", list_classes=[str(i) for i in range(n_classes)],
        normalize="prediction", ax=ax2)
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(20,8))
plot_cm(y_true=y_test, y_pred=prediction, title="Our Awesome Model", list_classes=[str(i) for i in range(n_classes)],
        normalize="prediction", ax=ax1)
plot_cm(y_true=y_test, y_pred=prediction_naive, title="Rolling Dice", list_classes=[str(i) for i in range(n_classes)],
        normalize="prediction", ax=ax2)
plt.show()

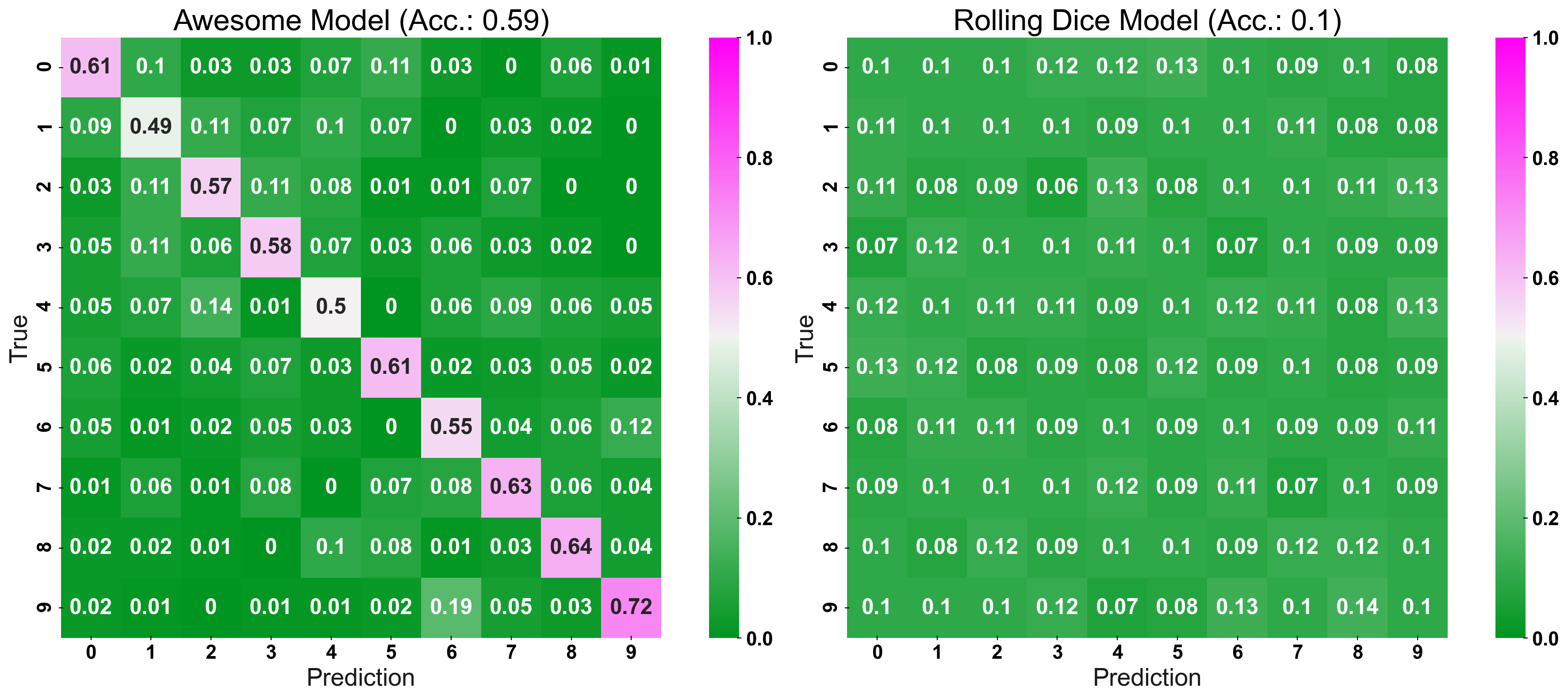
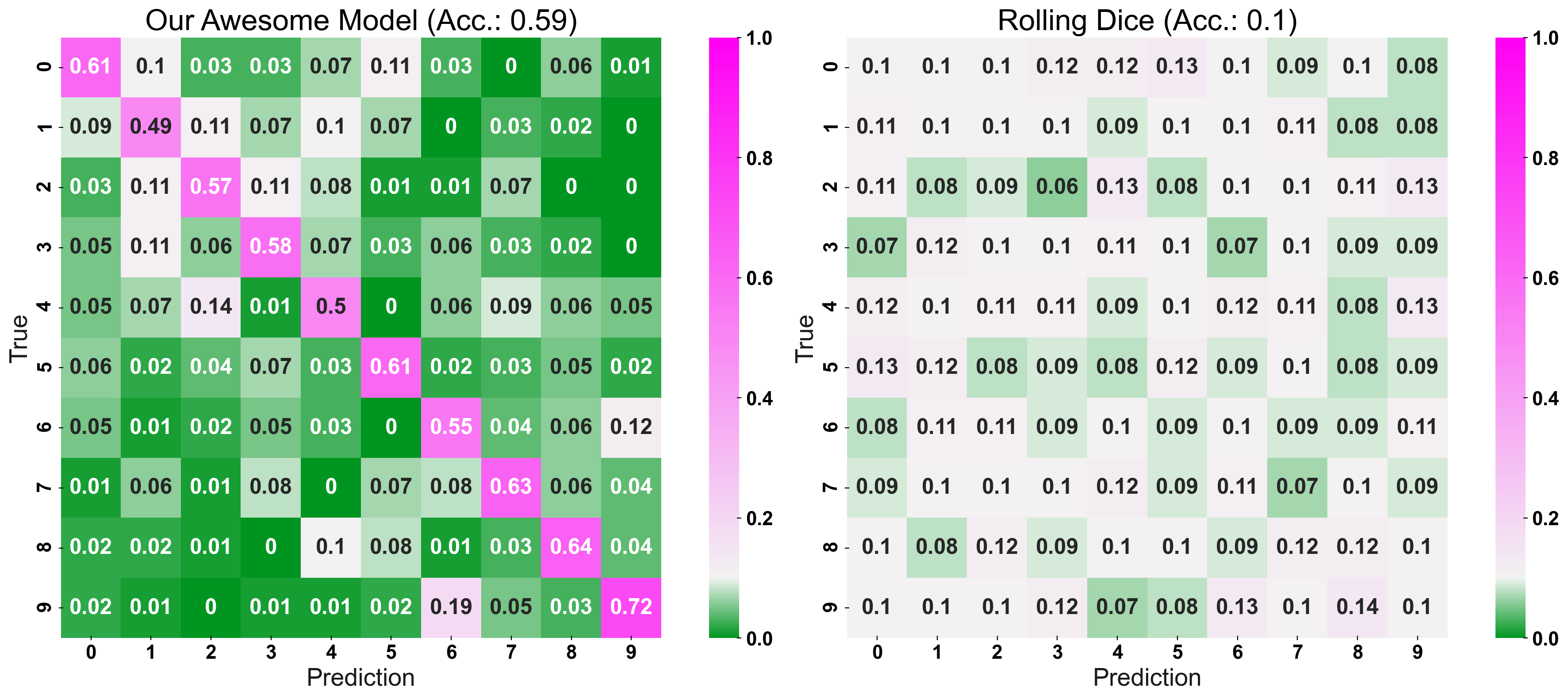
Conclusion to Confusion Matrix

I would like to share a few key takeaways from the article:

• Evaluate predictions of classification models with a confusion matrix
• For classifications, it is not only the accuracy matters but also the true positive/negative rate
• Evaluate your model relative to a naive baseline, e.g. a random prediction or a heuristic
• When plotting a confusion matrix, normalise the colour-bar relative to the performance of your naive baseline model
• A CCM lets you assess a model’s performance more intuitively, and is better suited for presentations than a regular confusion matrix

Frequently Asked Questions

Thanks for reading! Hope you liked my article on confusion matrix! 

The media shown in this article is not owned by Analytics Vidhya and is used at the Author’s discretion.

Finn Hoener

11 Apr 2023