This article was published as a part of the Data Science Blogathon.
Introduction
Cluster analysis or clustering is an unsupervised machine learning algorithm that groups unlabeled datasets. It aims to form clusters or groups using the data points in a dataset in such a way that there is high intra-cluster similarity and low inter-cluster similarity. In, layman terms clustering aims at forming subsets or groups within a dataset consisting of data points which are really similar to each other and the groups or subsets or clusters formed can be significantly differentiated from each other.
Why Clustering?
Let’s assume we have a dataset and we don’t know anything about it. So, a clustering algorithm can discover groups of objects where the average distances between the members/data points of each cluster are closer than to members/data points in other clusters.
Some of the practical applications of Clustering in real life such as:
1) Customer Segmentation: Finding a group of customers with similar behavior given a large database of customers (a practical example is given using banking customer segmentation)
2) Classifying network traffic: Grouping together characteristics of the traffic sources. Traffic types can be easily classified using clusters.
3) Email Spam filter: The data is grouped looking at different sections (header, sender, and content) and then can help classify which of them are spam
4)City-Planning: Grouping of houses according to their geo-location, value, and house type.
Different types of Clustering Algorithms
1) K-means Clustering – Using this algorithm, we classify a given data set through a certain number of predetermined clusters or “k” clusters.
2) Hierarchical Clustering – follows two approaches Divisive and Agglomerative.
Agglomerative considers each observation as a single cluster then grouping similar data points until fused into a single cluster and Divisive works just opposite to it.
3) Fuzzy C means Clustering – The working of the FCM Algorithm is almost similar to the k-means clustering algorithm, the major difference is that in FCM a data point can be put into more than one cluster.
4) Density-Based Spatial Clustering – Useful in the application areas where we require non-linear cluster structures, purely based on density.
Now here in this article, we will be deeply focusing on the k-means Clustering algorithm, theoretical explanations of working of k-means, advantages and disadvantages, and a solved practical clustering problem that will enhance the theoretical understandings and give you a proper view of how k-means clustering works.
What is k-means Clustering?
K-Means Clustering is an Unsupervised Learning algorithm, used to group the unlabeled dataset into different clusters/subsets.
Now you must be wondering what does ‘k’ and ‘means’ in the k-means Clustering means??
Putting a rest to all your guess here ‘k’ defines the number of pre-defined clusters that need to be created in the process of clustering say if k=2, there will be two clusters, and for k=3, there will be three clusters, and so on. As it is a centroid-based algorithm, ‘means’ in k-means clustering is related to the centroid of data points where each cluster is associated with a centroid. The concept of a centroid based algorithm will be explained in the working explanation of k-means.
Mainly the k-means clustering algorithm performs two tasks:
- Determines the most optimal value for K center points or centroids by a repetitive process.
- Assigns each data point to its closest k-center. Cluster is created with data points which are near to the particular k-center.
How does k-means Clustering work?
Suppose, we have two variables X1 and X2, scatter plot below-
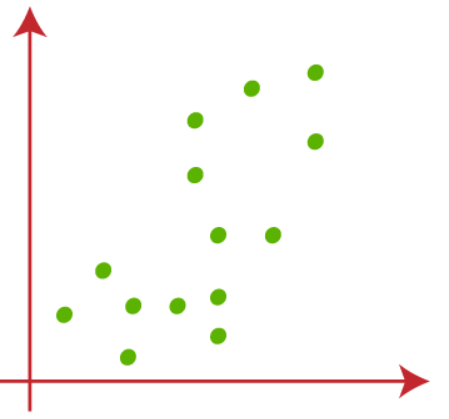
(1) Let’s take the value of k that is the number of pre-defined clusters to be 2(k=2), so here we will be grouping our data into 2 clusters.
Random k points need to be chosen to form the clusters. No restrictions on the selection of random k points can be from inside the data and outside as well. So, here we are considering 2 points as k points (which are not part of our dataset) shown in the figure below-
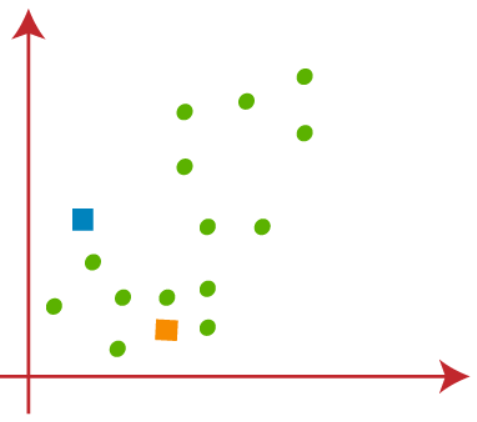
(2) The next step is to assign each data point of the dataset in the scatterplot to its closest k-point, this will be done by calculating Euclidean distance between each point with k point and draw a median between both the centroids, shown in the figure below-
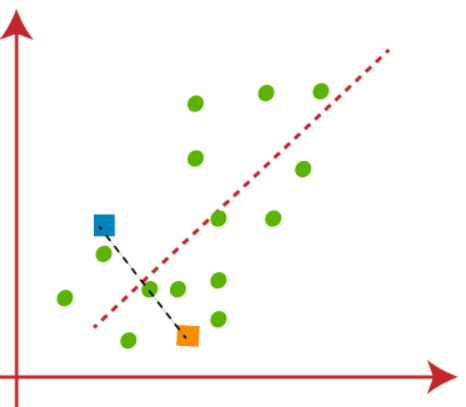
We can clearly observe that the point to the left of the red line are near to K1 or the blue centroid and the points to the right of the red line are near to K2 or the orange centroid.
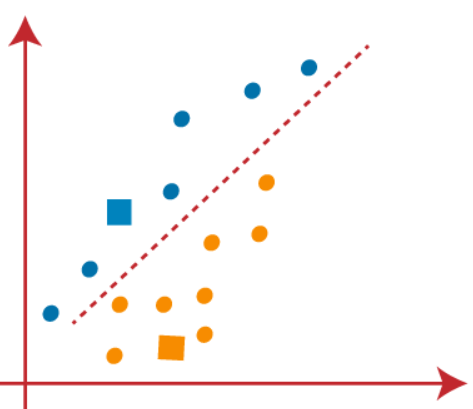
(3) As we need to find the closest point, so we will repeat the process by choosing a new centroid. To choose the new centroids, we will compute the center of gravity of these centroids and will find new centroids as below-
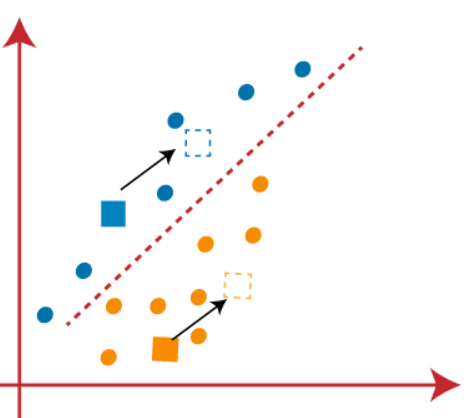
(4) Now, we need to reassign each data point to a new centroid. For this, we have to repeat the same process of finding a median line. The median will be like below-
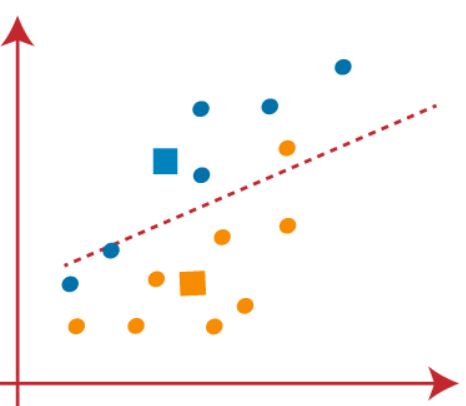
In the above image, we can see, one orange point is on the left side of the line, and two blue points are right to the line. So, these three points will be assigned to new centroids
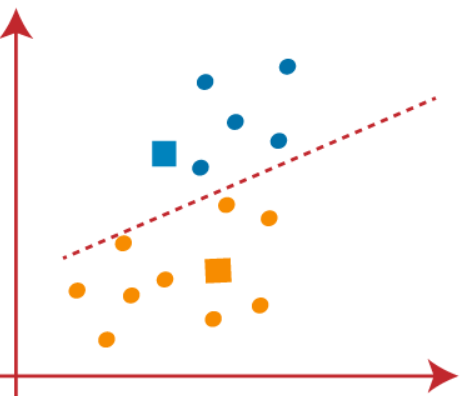
We will keep finding new centroids until there are no dissimilar points on both sides of the line
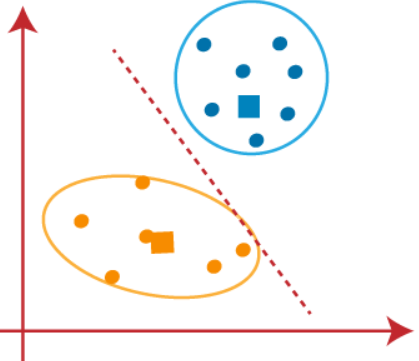
We can now remove the assumed centroids, and the two final clusters will be as shown in the below image
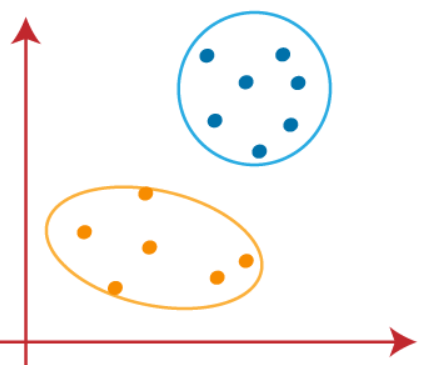
So, far we have seen how the k-means algorithm works and the various steps involved to reach the final destination of differentiating clusters.
Now you all must be wondering how to choose the value of k number of clusters??
The performance of the K-means clustering algorithm highly depends upon clusters that it forms. Choosing the optimal number of clusters is a difficult task. There are various ways to find the optimal number of clusters, but here we are discussing two methods to find the number of clusters or value of K that is the Elbow Method and Silhouette score.
Elbow Method to find ‘k’ number of clusters:[1]
The Elbow method is the most popular in finding an optimum number of clusters, this method uses WCSS (Within Clusters Sum of Squares) which accounts for the total variations within a cluster.
WCSS= ∑Pi in Cluster1 distance (Pi C1)2 +∑Pi in Cluster2distance (Pi C2)2+∑Pi in CLuster3 distance (Pi C3)2
In the formula above ∑Pi in Cluster1 distance (Pi C1)2 is the sum of the square of the distances between each data point and its centroid within a cluster1 similarly for the other two terms in the above formula as well.
Steps involved in Elbow Method:
- K- means clustering is performed for different values of k (from 1 to 10).
- WCSS is calculated for each cluster.
- A curve is plotted between WCSS values and the number of clusters k.
- The sharp point of bend or a point of the plot looks like an arm, then that point is considered as the best value of K.
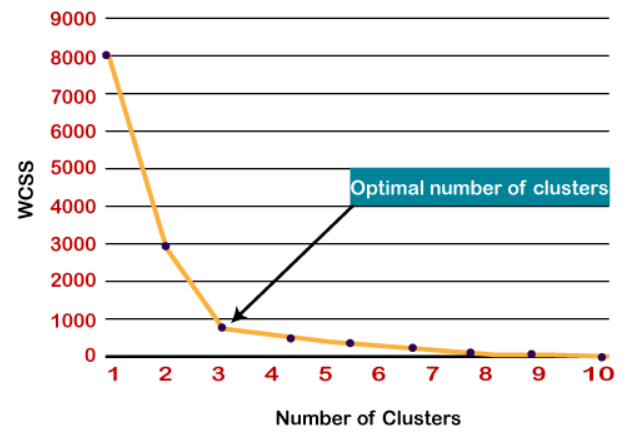
So here as we can see a sharp bend is at k=3, so the optimum number of clusters is 3.
Silhouette score Method to find ‘k’ number of clusters
The silhouette value is a measure of how similar an object is to its own cluster (cohesion) compared to other clusters (separation). The silhouette ranges from −1 to +1, where a high value indicates that the object is well matched to its own cluster and poorly matched to neighboring clusters. If most objects have a high value, then the clustering configuration is appropriate. If many points have a low or negative value, then the clustering configuration may have too many or too few clusters.
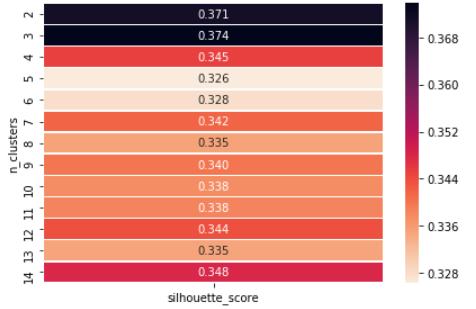
Example showing how we can choose the value of ‘k’, as we can see that at n=3 we have the maximum silhouette score hence we choose the value of k = 3.
Advantages of using k-means clustering
- Easy to implement.
- With a large number of variables, K-Means may be computationally faster than hierarchical clustering (if K is small).
- k-Means may produce Higher clusters than hierarchical clustering.
Disadvantages of using k-means clustering
Difficult to predict the number of clusters (K-Value).
Initial seeds have a strong impact on the final results.
Practical Implementation of K-means Clustering Algorithm using Python (Banking customer segmentation)
Here we are importing the required libraries for our analysis.
Reading the data and getting top 5 observations to have a look at the data set
The code for EDA (Exploratory Data Analysis) has not been included, EDA was performed on this data, and outlier analysis was done to clean the data and make it fit for our analysis.
As we know that K-means is performed only on the numerical data so we choose the numerical columns for our analysis.

Now to perform the k-means clustering as discussed earlier in this article we need to find the value of the ‘k’ number of clusters and we can do that using the following code, here we using several values of k for clustering and then selecting using the Elbow method.

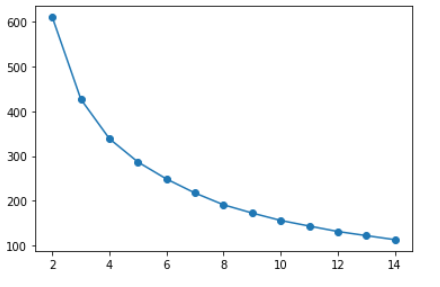
As the number of clusters increases, the variance (within-cluster sum of squares) decreases. The elbow at 3 or 4 clusters represents the most parsimonious balance between minimizing the number of clusters and minimizing the variance within each cluster hence we can choose a value of k to be 3 or 4
Now showing how we can use the Silhouette value Method to find the value of ‘k’.

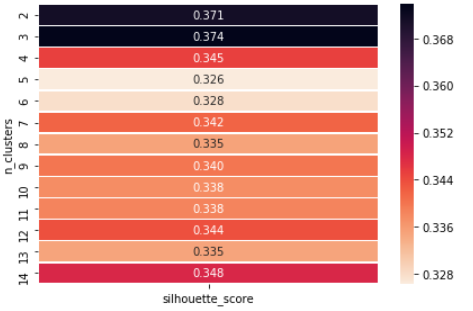
If we observe, we get the optimum number of clusters at n = 3 so we can finally choose the value of k = 3.
Now, fitting the k means algorithm using the value of k=3 and plotting heatmap for the clusters.

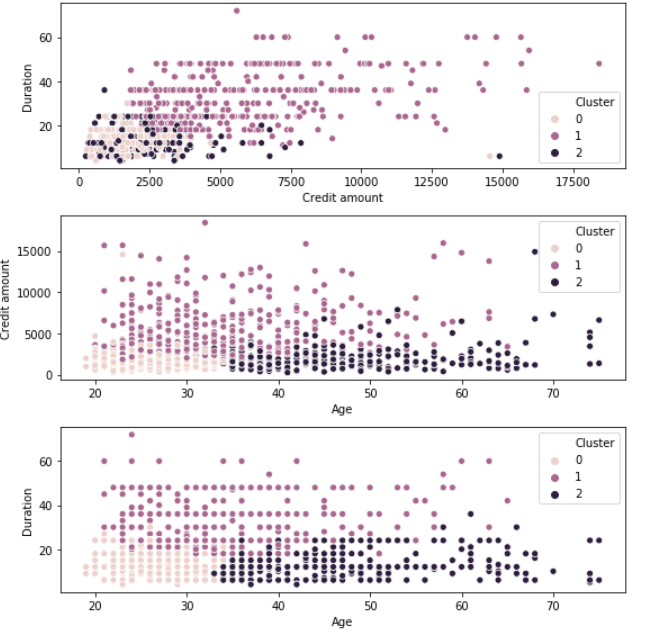
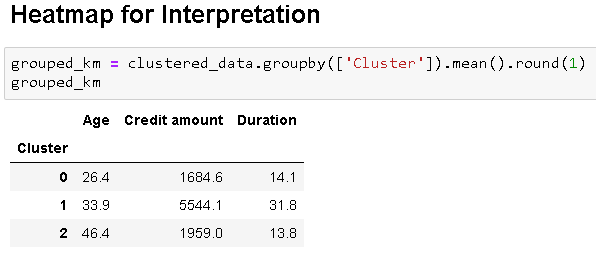
Final Analysis
Cluster 0 – Young customers taking low credit loans for a short duration
Cluster 1 – Middle-aged customers taking high credit loans for a long duration
Cluster 2 – Old aged customers taking medium credit loans for a short duration
Conclusion
We have discussed what is clustering, its types, and its’s application in different industries. We discussed what is k-means clustering, the working of the k-means clustering algorithm, two methods of selecting the ‘k’ number of clusters, and are advantages and disadvantages of it. Then we went through practical implementation of k -means clustering algorithm using Banking Customer Segmentation problem on Python.
References:
(1)img(1) to img(8) and [1] ,reference taken from “K-Means Clustering Algorithm”
https://www.javatpoint.com/k-means-clustering-algorithm-in-machine-learning




